Editor | On 25, Jun 2006

Edited by: Leora C. Slocum*, Micaiah C. Slocum, and
Hosannah M. Slocum
(*contact at leora@slocumfamily.org)

Most children like making soap bubbles and films, and experimenting with them, so let’s do our first experiment with soap films. Make wire frames of different configurations (you can use wire hangars, for example), prepare soap solution (formula listed below), immerse these frames in soap solution, take them out, and examine the results. In Fig.1 you can see that the soap film copies the geometry of the wire frame.

Bubble formula:
1 part karo syrup or glycerin
4 parts dishwashing detergent (i.e., Dawn Ultra)
16 parts water (distilled works best)

Fig.1. Plane wire frame after immersing in soap solution and taking it out Free Internet Wikipedia Encyclopedia

Now immerse a spatial frame in the soap solution, and you will make wonderful three-dimensional structures, as are the examples in the pictures below.

Fig. 2. Spatial wire frames after immersing in soap solution and taking them out Free Internet Wikipedia Encyclopedia

One very practical property of the soap films is that their surface areas are minimal, which engineers and architects use (the “soap film method”) to optimize future structures. They find that, in all cases, the surface area is minimal (the principle of surface energy minimum). So, soap films are not only toys for children, but also a very effective and very simple tool for engineers and architects. When doing your experiment, try to make wire frames of unusual form, and observe what soap structures you’ll get. We would love to have pictures of your soap film configurations for our “Student’s Corner Online Museum”.

A soap bubble consists of a thin spherical shell, which is composed of water and soap ions. Inside the shell is air or gas at greater pressure than the external atmospheric pressure because of the film tension and curving configuration. Students interested in a more detailed explanation of the physical reason of this excess of pressure could read a very interesting book “The Science of Soap Films and Soap Bubbles,” written by one of the greatest scientists and promoters in this realm of science – Professor Cyril Isenberg.

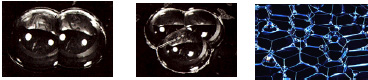
Free soap bubbles are spherical in shape and consist of a thin shell of water with surfactant molecules on each surface. Bubbles contain some amount of air, or gas, at a pressure that is greater than the external pressure. Another interesting configuration results when “a bubble meets a bubble”, as observed in Fig. 3 below.

Fig. 3. Results of meetings between soap bubbles. a – two bubble cluster; b – three bubble cluster; c –many-bubble cluster Free Internet Wikipedia Encyclopedia

Now let us consider their practical applications. We’ll start with making models of devices and processes from the Nuclear Physics realm. How are soap bubbles and nuclear devices connected?
We hope that you had heard such terms as annihilation of elementary nuclear particles, and Geiger-Muller sensor of radioactivity. How to illustrate work of such “systems” in the possible simplest way? Author was thinking about this question since university times, and as a result we can consider a simple model, in which soap bubbles are used as models of nuclear particles. The basis to such presentation is analogy – soap bubbles as result of their collision disappear, elementary particles also could disappear after their collision. Demonstration model of annihilation of elementary particles is shown in Fig. 4.

Fig. 4. Demonstration Model of Process of Nuclear
Particles Annihilation
1 – soap bubbles generator; 2 –charged plate;
3 –electrical battery; 4 – second soap bubble generator;
5 –second charged plate; 6 – heating element; 7 – faucet.
Public Domain – SU Patent #1,223,272

Demonstration Model contains an imitator of charged particles, which is made as two generators of soap bubbles, under which metal plates are placed. These plates are connected with one of electrical poles of battery. Imitator of annihilation process is made as heating plate. To start modeling process the battery 3 is switched on, and as result plate 2 got a negative potential, and plate 5 – positive. At the same time faucets 7 are opened. Soap drops, passing plate 2, are charged negatively, and drops passing plate 5, are charged positively.

Contrary charged soap bubbles are attracting to each other, and a result of their collision bursts. Bursting is accompanied with specific sound. In this way soap bubble illustrates invisible process of annihilation of elementary particles. As “Inventive Homework” we propose you develop, or in other words invent, using soap bubbles – demonstration model of Geiger-Muller elementary particle counter. We kindly ask members and visitors of Our Student’s corner to take a try in developing such a demonstration model. And, please, inform us about results.

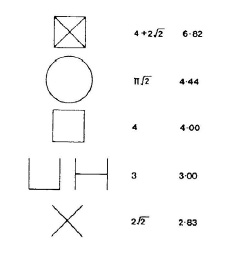
We could also use the property of minimum surface area of a soap film to solve other optimization problems. The most famous of these is the “Motorway problem” or Jacob Steiner Problem, discovered about two centuries ago by Jacob Steiner. Consider the problem of linking four towns A, B, C and D by a road. The towns are located at the corners of a square. What would you think would be the shortest path to get through all four towns? Let’s consider some possible solutions. Different options of a network that will enable us to travel from any town to any other town by the shortest possible route are shown in the schemes below.
1. Consequent way “from-town-to-town” by sides of a square, with cross-section roads:
4 + 2 2 = 6.83
2. A circular road passing through A, B, C and D has a length of:
2 ) 4.44
2
2Ï€( 1 =
3. If a straight line replaces each circular arc, this produces the square roadway configuration with a length of 4.00;
4. The further reduction in length can be made by removing the road on the sides of the square to give a U or H shape, which in both cases will have the length of 3;
5. One might think that the shortest road is the crossroad system, with a length of 2 2 = 2.83 . But is it? The table of possible routes and corresponding distances is shown below:

Fig.5. Optimal Route (a) and Scheme of Experiment (b) for Motorway Problem
Using soap films, as shown in Fig.5b, they found that the route is minimal when the angle between the roads is 120°, and, as a result, the minimal possible total length is 1 + 3 = 2.73 , which is about 4% shorter than the crossroad system. It is a general property of the solutions to these problems that they consist of straight lines forming a number of intersections. In order to reach an analogical solution, which will take advantage of the soap film unique feature of reducing surface space to minimum, we can construct two parallel clear plexiglass plates joined by four pins, perpendicular to the plates, arranged at the corner of a square which will represent the four towns. When this arrangement is immersed in a bath of soap solution and withdrawn from the bath, a vertical soap film will be formed between two plates. Optimal structure of Motorway was determined!

The sixth crew of the International Space Station (November 2002 – May 2003) also performed an experiment with bubbles, where astronauts immersed different shaped wire frames into soap grout and observed the configuration of the soap film. They took the famous book “Soap Bubbles” written by Charles Boins, (the first edition was published approximately 100 years ago – in 1911! The advantage of taking this book was, of course, that this book was also published in Russian.) Responsible for providing this experiment was US Astronaut Donald Petty, who prepared some soap solution by mixing his shaving cream in distilled water (2,5%) and added 15% of glycerin. Then he made a round expandable loop from thin wire to insert into a vessel with a narrow neck, which contained soap solution. After taking it out, and moving the wires apart, he could observe interference patterns. But, first he used only distilled water to avoid filling the space station with soap films and bubbles. To his surprise, there was a water film on the 53 mm loop! He estimated its thickness to be approximately 300 micrometers (about one third of a millimeter), which is noticeably bigger than the thickness of usual soap films. The volume of this water film, calculated by the thickness and diameter, was about 660 cubic millimeters. The water film showed high strength, and was able to maintain expanding strength up to a diameter of 115 millimeters, while its thickness lowered up to 60micrometers (50 times more than the thickness of regular soap films). Interested members of the Student’s Corner can find more information about the experiments with films on the NASA website.

Now we’ll describe two experiments with soap films and bubbles in other extreme conditions – under low temperatures. One of my favorite professors of Kharkov State University in Ukraine, Jacob Geguzin, contributed a lot in Solid State Physics, including the following experiments:

First Experiment: Put a vessel with soap solution in freezing temperatures (outside in winter or a walk-in freezer), and blow up a soap bubble. Immediately you’ll see small crystals, which quickly expand, and finally come together. As soon as the bubble completely becomes frozen, a dent will appear in the top of the tube. Air in the bubble is more frozen in the lower part of the vessel because the top of the bubble is located in the less frozen part of the tube. The direction of the crystallization process is from the bottom to the top. The air inside the bubble is frozen quicker and the dent becomes bigger.

Second Experiment: On a day with freezing temperatures and access to snow, blow a soap bubble. Let it burst. Repeat this “test” to be sure that the soap bubbles are not freezing under this temperature. Now prepare a snowflake. Blow a soap bubble, and immediately throw the snowflake on the soap bubble. The snowflake will immediately slide to the bottom of the soap bubble. The place, where the snowflake would stop, would become center of crystallization, and cause the whole bubble to be frozen.

The color of soap bubble walls depends on their thickness. Initially, a soap bubble is transparent, but while the bubble increases in size, colors appear – first violet, which appears while the thickness of the soap film equals 210 nm (nanometers), then subsequent colors of the rainbow, as the thickness of the soap film continues to decrease, and finally a black spot appears.

Fig.6. Rainbow
Courtesy of Free Internet Wikipedia Encyclopedia

At this point the thickness of the soap film (5 nm) is less than the wavelength of visible light making the film is invisible. If the thickness would decrease a little more, the surface force disappears, and the soap bubble collapses. Such thin films, with thickness in 1-2 molecules, have a special title, “monomolecular layers”. Experiments have shown that 10 liters of this special solution are enough to create a film with a surface area 2,710,000 square meters and completely invisible to the naked eye!

In conclusion to the Student’s Corner #6, we propose that our members attempt a problem about sop films from Professor Edward Teller, the Father of US Hydrogen Bomb. The problem is as follows: “Try to use a grain of soap to spread a film over a big area of water. It is surprising how much territory a little soap can cover. But there is a limit. In the end, you’ll have put a “monomolecular layer” of soap on the surface of the water. If I do the same experiment with oil that produces a monomolecular layer, then I can deduce the diameter of molecule of oil. This, of course, gives a very crude value for the size of the molecule.” Try to estimate the size of “participating molecules” by doing a similar soap film experiment. For advice and assistance, read through Professor Edward Teller’s book “Conversations on Dark Secrets of Physics.”

Happy Inventing!
Editorial staff for this article: Leora, Micaiah (13), and Hosannah (11) Slocum. The Slocum Family is pleased to be involved with The TRIZ Journal and have incorporated these editorial activities into their home school education program.