Editor | On 18, Jun 2006

Sankt-Petersburg State University of Information Technologies,
Mechanics and Optics,
Department of Control Systems and Informatics
Sankt-Petersburg, Russia
E-mail: bushuev@inbox.ru

Introduction
This is a third paper from series of work [1,2] on mathematical invention problem models. The Author has got several questions and remarks after two articles. Principal question and remark are next:
1) “Wherefore mathematical model of technical contradiction (or Su-Field) needed?”
2) “ARIZ has two kinds of operators: logical operator processes the problem strictly and psychological operator processes the inventor. It is necessary to simulate the process, occurring with the technical object actually, but contradiction is psychological operator and artificial construction. Simulation of contradictions can bring to a mysticism”.
The answer to question is short. Quantitative evaluation of mentation is chief aim. Model gives a chance to connect invention psyche and success of problem solving, recommendations on educating technical creativity.
The answer to the remark requires more detailed explanations. We can simulate technical system-prototype. This system function real, let bad, and ARIZ not needed for its simulation. It is necessary to know only the physical laws for dynamic description. Analogously, we can simulate real new technical system, but previously it is necessary to find a solving of invention problem. If the solving is absent, the real new technical object is absent too. Therefore it can be not simulated. It is possible to simulate an evolution of system quality in invention problems.
Mathematical model requires operators, variables, relationships for the description of decision process. These terms gives ARIZ [3] , since it is the best logical and psychological model of solving process. Logical operators of ARIZ are the input controls, but psychological operators are the parametric controls for mathematical model. These controls enter in consciousness of inventor and are mixed into united model. Therefore mentation of inventor is coupled with process of technical system evolution from prototype towards new solution. They are not separated inwardly consciousnesses. Mathematical evolution model is a mathematical thinking model.
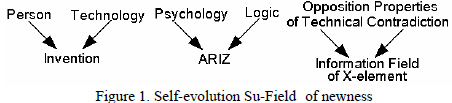
In this sense an approach of Author is not differed from the G. Altshuller’s approach. G. Altshuller has invented ARIZ at the turn of psychology and logic (Fig.1, in the middle). This synthesizing process of the new formations is presented by Self-evolution Su-Field [2] .

Figure 1. Self-evolution Su-Field of newness

Relative to mysticism: thinking contains a mystic. ARIZ is not an exception. Ideal Final Result is a mystic element too. Simulation of the creative thinking is impossible without mystics.

Mathematical Model of Search Motions

Statement of Problem
The mathematical model of the Self-evolution Su-Field was offered in [2] .
The Self-evolution Su-Field (Fig.1, on the right) has two stages of evolution:
1.Embryonic growth of X-element (or “pregnancy” for opposite properties of technical contradiction).
2.Birth and existence of X-element.
On first stage an evolution is imitated by differential equation system
K dx/dt = – 3xy – ay, (1)
K dy/dt = 3xy – ax, (2)
where x and y – evolutional coordinates of opposite properties, for instance,
maneuverability and comfortability for transport, K and a- parameters,
characterizing properties of thinking.
On second stage an evolution is simulated by differential equation system
dx/dt = – (k1/v) xy + k-1z, (3)
dy/dt = (k1/v) xy – k-1z, (4)
dz/dt = (k1/v) xy – k-1z, (5)
where evolutional coordinate z reflects the information property of X-element,
v, k1, k-1- parameters, characterizing properties of thinking. The geometric structures of Su-Field are presented in accordance with (1) – (5) (Fig. 2).

Figure 2. Structure of Self-evolution Su-Field transformation

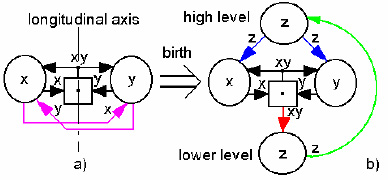
a) embryonic stage; b) stage of birth and existence
Pay attention to the Su-Field form of the differential equations. Derivatives in left parts (1)-(5) are marked by the circles with corresponding coordinate inwardly.
The coordinates or variables x, y, z in the right of parts (1)-(5) are marked by arrows. The arrow is identified x, if it comes out of the circle x. The arrow x falls into the circle y, if variable x exists in the right of part of equations for the derivative dy/dt. Factors and signs (plus or minus) of variables can be any in the Su-Field analysis. The square with the internal point is a mathematical product xy.
Positive and negative S-curves are a decision of equations (1)-(2), but the equations (3)-(5) simulate a old S-curves disintegration and generation of new Scurve for X-element.
There is a mutual struggle or homeostasis between opposite properties x and y through lilac arrows in the Fig.2а. On the second stage this struggle brings the Xelement with coordinate z (Fig.2b). At first X-element will be born in the subconscious (lower circle for z in the Fig.2b), next it moves over to the consciousness (upper circle for z).
Let us raise a question: “What motions bring a generation of X-element in the subconscious?” There is a suggestion [1] that the motions must be some search random oscillations.
Why they are oscillations?
Because homeostasis has continuous interchange of energy and information between opposite properties.
Why they are random oscillations?
ARIZ give a direct systematic searching. This searching displaces a cut-and try method from the consciousness into the subconscious, but a cut-and-try method has the random walk and hunting.
We shall use structured syntheses in order to find the mathematical equations of search oscillations.

Structured Syntheses of Search Su-Field
It was stated already, that equation system (1)-(5) is a mathematical model of Su-Field. Now shall suppose that Su-Field (Fig.2) is a structured model of equation system. The structure changes if someone includes and excludes elements and relationships. New structure can be named by search Su-Field. This Su-Field must be installed between Fig.2a and 2b, because X-element has come up for the subconscious already (the circle z on the lower level in Fig.2b), but it did not come up for the consciousness else (the circle z on the high level in Fig.2b). Thereby left Su-Field (Fig.2a) is a predecessor of search Su-Field.
Let’s to consider the structure of this predecessor. Determination of the internal relationships is the first problem. Right part of equations (1)-(2) can be recorded by standard type
dx/dt =c1xy + c2x+ c3y, (6)
dy/dt =c4xy + c5x+ c6y. (7)
Standard type will be easy transformed in concrete type , e.g. for coordinate x (equation (6)) c1=-3/K, c2=0, c3=-a/K, for coordinate y (equation (7)) c4=3/K, c5= -a/K, c6=0.
Shall suppose that product xy is an ability of variables x and y to reproduction. In population theory the product xy defines quantity of the pair meetings for persons of different sexes, but c1 (or c4) is birth rate factor. The summands c3y for variable x and c5x for variable y reflect an influence of one coordinate on other coordinate. Unity and struggle of oppositions, i.e. mutual existence or homeostasis, is realized through these relationships. Insertion its coordinate ( c2x for x and c6y for y) brings a liberty of evolution. Mathematically the summands xy and c3y give a forced motion for x, but summand c2x gives a natural motion for x.

Searching of new relationships is a second problem now. Let’s to take a look at the structure of Su-Field-predecessor (Fig.2a). This structure is absolutely symmetrical on longitudal axis. However self-organization brings about the loss or reducing degrees of symmetry. For instance, before crystallizations a liquid is a homogeneous and isotropic substance, i.e. completely symmetrical. After the congelation a liquid has directions of crystalline lattice, i.e. degree of symmetry is lowered. So let’s to break a symmetry of Su-Field.

How to destroy a symmetry, this is a question. The answer can give analogies, ARIZ, intuition, finally. In work [2] embryonic growing of X-element is named by the stage of pregnancy for opposite properties of technical contradiction. Consequently, let’s name one opposite property a “Father”, then other opposite property must be identified a “Mother”, but X- element must be identified a “Baby”. For instance, circle x in the Fig.2 is a “Father”, but circle y is a “Mother”.
Next there is usefulness to remember Step 1.4 of ARIZ-85B. Step 1.4 recommends choosing of one of the conflict sides, which provides the best performance for the main useful function of the system. Let this alternative is a “Father”. That signifies this choice?
1. This is breaking a symmetry between Su-Field’s elements x and y,
2. In [1] it was stated already, that Step 1.4 was a beginning of conflict resolving. Mathematical sign of X-element was chosen, but its matter was stayed unknown. Now becomes clear this choice is not only mathematical sign as well as sign of appearance of X-element in the subconscious. Its own motion is reflected by the loop z from B to B. This transformation is provided in the Fig.3.

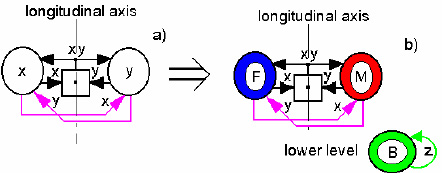
Figure 3. Transformation of Su-Field’s structure
a)stage of conception; b) stage of Baby’s appearance in the subconscious: F –
“Father”, M – “Mother”, B – “Baby”.

Reinforcement of conflict occurs on Step 1.5. State of “Father” intensifies.
The main useful function is completely performed, i.e. this side of conflict is resolved. “Father” has done its deal, now “Father” can walk. He gets an own motion. So the summand c2x appears in the equation (1), but a loop x from F to F appears in the structure of Su-Field (Fig.4b) . “Mother” temporarily loses ability to reproduction since she carries “Baby”. So a product xy disappears in the equation (2), and black arrow xy disappears at the input M also, but at the same time a red arrow y appears from M to B.
Consider a Step 1.6 of ARIZ. X-element must be found and it must exclude harmful side of conflict, so “Baby” and “Mother” must enter in homeostasis. Consequently, green arrow must pass from “Baby” to “Mother”. Then red arrow from M to B will mean an embryonic growing or searching of “Baby” by “Mother”, but green arrow from B to M will mean an eliminating a “Mother” by “Baby”.

Figure 4. Structure of search Su-Field

a)stage of X-element’s appearance in the subconscious; b) stage of searching Equation system for stage of searching can be written now. We have a system from Fig.4b:
dx/dt = c1xy + c2x+ c3y, (8)
dy/dt = c5x+ c7z, (9)
dz/dt = c8y + c9z. (10)
Let’s to redefine variables in equations (8)-(10): y=x1, z=x2, x=x3. Substitution gives following result:
dx1/dt = – x2 – x3, (11)
dx2/dt = x1+ σ1×2, (12)
dx3/dt = σ2×1 – σ3×3 + x1x3, (13)
where σ1=c9, σ2=c3, σ3= – c2 , but c1 =c8 =1, c5 = c7 = -1 in (8)-(9).
The equation system (11) – (13) defines known chaotic RÅ‘ssler’s attractor [4] .
3-d plot of attractor is submitted for the Fig.5a.

Figure 5. Chaotic RÅ‘ssler’s attractor
a) 3-d plot, b) homoclinic orbit
Аttractor demonstrates a screw chaos under σ1=0.38, σ2=0.3, σ3= 4.5.

Paths begin on both sides from unstable stationary point of type “saddle-focus”, as there is homeostasis between “parents”. But attractor is asymmetrical, as the homeostasis between “Mother” and “Baby” breaks symmetry. There is homoclinic orbit inwardly attractor, which penetrates saddle-focus. This orbit very unstable and sensitive to changing the parameters σ1, σ2, σ3. Probably it is model of new idea, which revolves in brain, but until it is possible to jump at the idea.

Figure 6. Structure of homeostasis in search Su-Field

Fig. 6a,b gives transition to usual writing a search Su-Field. The Su-Field has double homeostasis: H1 is a homeostasis between opposite properties of contradiction S1 and S2, but H2 is a homeostasis between the Information Field (Finf) of X- element and S2. Search coordinate motions are provided in the Fig. 6c. Homeostasis between S1 and S2 is powerfully distinguished from the homeostasis between S2 and Finf. The substance S1 is deviated to one side only, as far as other side of conflict is resolved.
Homeostasis between S1 and Finf is absent, since X-element must not disturb to substance S1. State of substance S1 ensures a main useful function of the system. Then there is a question how to simulate a situation, when X-element helps to substance S1? Step 1.6 of ARIZ has such possibility. Help is not a mutual struggle, so homeostasis between S1 and Finf must be absent. However a supporting relationships must pass from Finf to S1. RÅ‘ssler’s attractor has no such relationships. Let’s take chaotic Lorenz’s attractor. It has equation system
dx1/dt = – σx1 + σx2, (14)
dx2/dt = rx1 – x2 – x1x3, (15)
dx3/dt =- bx3 + x1x2. (16)
Attractor gives chaotic oscillations under σ=10, b=8/3, r≥27.74. Let’s to redefine variables in equations (14)-(16): x1=z, x2=y, x3=x. In such case structured scheme for equations (14)-(16) is provided in the Fig.7

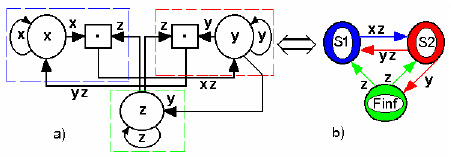
Figure 7. The homeostatic structure of Lorenz’s attractor

Lorenz’s attractor is transformed in search Su-Field (Fig.7b) also as a RÅ‘ssler’s attractor. However structure of opposite properties S1 and S2 is the another in the Lorenz’s attractor. Opposite properties S1 and S2 are symmetrical in the first place, secondly mutual blows are yz and xz.
The Su-Field has double homeostasis too: H1 is a homeostasis between opposite properties of contradiction S1 and S2, but H2 is a homeostasis between the Information Field (Finf) of X- element and S2. Homeostatic motions are provided in the Fig.8. Homeostasis between S2 and Finf (or “Mother” and “Baby”) is much coordinated. “Baby” copies “Mother” practically (Fig.8b). So product yz (Fig.8c) has one and same sign (yz > 0), and blows on the “Father” are unidirectional oscillations in the homeostasis H1. “Father’s” motions (x in Fig.8a) are bilateral oscillations with respect to a steady component. Consequently generation of steady component is a help from the X- element to substance S1. Due to this search possibilities are increased in contrast with the RÅ‘ssler’s attractor. Substance S1 has only unidirectional oscillations in the RÅ‘ssler’s attractor.

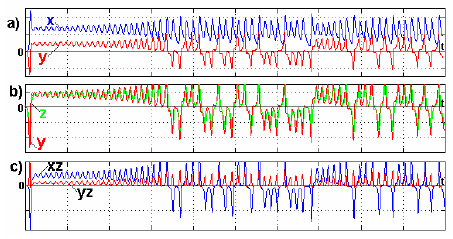
Figure 8. The homeostatic motions in Lorenz’s attractor

Conclusion
Main results of this paper are next:
1. Mathematical model of the search Su-Field.
This model simulates possible creative thinking in conditions of the Xelement’s searching. It is a chaotic RÅ‘ssler’s attractor or Lorenz’s attractor.
Global compression under local instability leads to the chaotic attractor [5] . Tapering chain of contradictions (administrative, technical, physical) is a global compression in the ARIZ. Some steps and jumps between steps of ARIZ give local instability.
2. Method of structured syntheses for the differential equation system.
Method is based on the Su-Field analysis. Derivatives in left part of equations are the elements of Su-Field, but the items in the right of part are relationships of Su-Field. Signs and factors are not taken into account.
3. Structured chaotic attractor model.
This model is a double homeostat with asymmetrical relationships.

References
1.Bushuev A. Technical Contradiction Control on Invention Problem. The TRIZ Journal, December 2004
2.Bushuev A. The Dynamic Substance-Field Analysis in ARIZ. The TRIZ Journal, December, 2005
3.Altshuller G.S., ‘To Find an Idea: Introduction to the Theory of Inventive Problems Solving’. – Novosibirsk, Nauka, 1986
4. Nicolis G., Prigogine I. Exploring Complexity. An introduction. New York: W.H.Freeman, 1989
5. Shuster H. G. Deterministic Chaos. Physik-Verlag, Weinheim, 1984