Editor | On 09, Feb 2003

By: Darrell Mann

Darrell Mann
Director, CREAX nv
Ieper, Belgium
Phone/Fax: +44 (1275) 342960
E-mail: darrell.Mann@creax.com

Introduction
This article forms the first in a series of three discussing the importance of systems that incorporate solutions incorporating the word ‘self’ – self-cleaning, self-balancing, selfaligning, etc – in the context of their relationship – in the true TRIZ sense – to the concept of ideality. This first article discusses the state of the art regarding technical system design solutions achieving self-x delivery of useful functions. It comes as a result of an extensive analysis of the US and other patent databases. The second article in the series will present a number of examples of systems in which ‘self’ has been successfully used to achieve a more ideal solution, while the third article in the series will shift its focus to the equivalent importance of ‘self-x’ systems in a business and management context.

Ideality and Self-X
Anyone that has used the Ideal Final Result (Reference 2, 3) part of the TRIZ suite of tools will have come across the word ‘self’. If we accept that the Ideal Final Result occurs when we achieve the desired function without cost or harm, then we often derive statements like ‘the system achieves the function itself’, or ‘the problem resolves itself’ when conceptualising ideal solution directions. Although in practice we may have to back away from such an ideal end point, there is a growing database of solutions where others have not. Systems that have solved problems ‘by themselves’ represent an important part of the global knowledge database.

This article is about such solutions. Taking the US patent database as its start point, the article examines the range of solutions featuring ‘self-X’ properties, where X may be just about any useful function other inventors have required a system to perform. Before examining the patent database in detail, however, it is first necessary to clarify the relationship between ‘things that do things for themselves’ and the TRIZ concept of ideality. We must do this, because examination of the patent database quickly reveals a large number of ‘self-X’ solutions that have little in common with the concept of an Ideal Final Result solution.

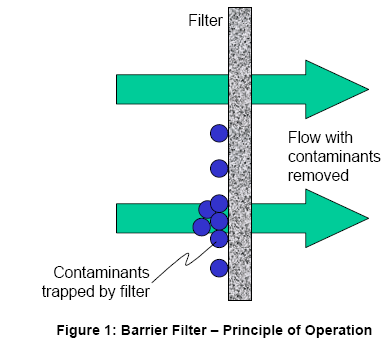
By way of example, we will look first at the case of barrier filters. The main useful function of a barrier filter is to separate contaminants of varying descriptions from a flow of air or oil or other substance – Figure 1. Barrier filters are used in a massive variety of industries in a wide variety of different roles. While in many senses sophisticated at the sub-system level, barrier filters are a nevertheless relatively crude means of achieving the desired separation function when examined as a system – they are bulky, fragile, block-up easily, and their performance worsens considerably after they have been collecting debris for a period of time. Because of these last two effects in particular, significant efforts have been expended in achieving ‘self-cleaning’ barrier filters.

In its standard form, a barrier filter is relatively easy to design and install. The main challenges faced by the designer involve achieving an acceptable flow through the surfaces of the filter, and ensuring that there are no leaks or air escape routes which would allow contaminants to inadvertently by-pass the filter.

The majority of ‘self-cleaning’ barrier filters operate by essentially reversing the direction of flow through the filter such that instead of being pushed against the barrier by flow in the normal direction (green arrows in the figure), the contaminants are pushed away from the filter by a flow in the other direction. This flow reversal is usually known as ‘back-washing’ or ‘back-flushing’. Although successful (to varying degrees) in ‘cleaning’ the filter, introduction of a ‘self-cleaning’ capability usually means a considerable increase in the complexity of the overall filtration system. It means, for example, that we need to introduce a means of reversing the flow; it means introducing means of capturing the contaminants that get blown away from the filter; it means ensuring that the seals we use to ensure they work in one direction now have to work in two; and it means addition of a considerable amount of hard (and often soft) ware to work out or tell the user when to conduct a back-flush operation. So, although we may have introduced a ‘self-cleaning’ capability – i.e. the filter assembly cleans itself, we have not necessarily derived an ‘Ideal Final Result’ solution because the system has become markedly more complex.

How, then, do we discriminate between such a ‘self-cleaning’ design and what TRIZ might define as an Ideal Final Result ‘self-cleaning’ design?

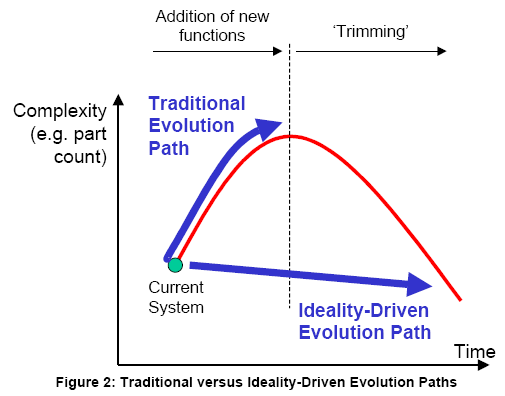
One useful way derives from the trend of evolution in which systems are seen to evolve in such a way that they must become more complex (in this case, we mean ‘increase their number of component parts’) before they can become simple again. Figure 2 illustrates the basic characteristic (see also Reference 1) of ‘part count’ versus time for a typical system.

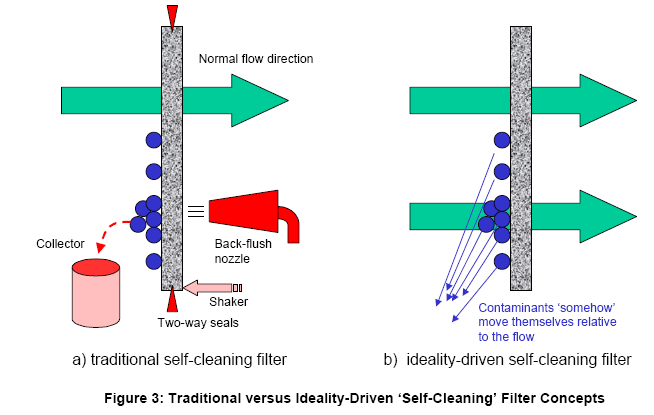
Thus we see that the current ‘state of the art’ ‘self-cleaning’ filter designs have followed the traditional evolution path which implies that if we add new functionality – in this case ‘cleaning’ – then the system must become more complex. Conversely, a ‘self-cleaning filter’ conceived from an ideality-driven route would get us to think much harder about whether or not it is possible to achieve ‘self-cleaning’ without complicating the system.

TRIZ, in other words, gets us to think rather harder about bypassing the traditional ways of doing things. The traditional way of doing things gives us a state of the art illustrated in Figure 3a. It bears little relation to the IFR-driven ‘self-cleaning’ filter shown in Figure 3b. The ‘real’ (ideality-driven) ‘self-cleaning filter’ – where the filter material really ‘cleans itself’ may not be possible today (actually it may be – it just may not be a barrier anymore), but the big point is that at least we should ask the question.

Connection With Function Analysis and ‘Trimming’
It is perhaps useful to re-examine these two alternative filter design concepts from the perspective of function analysis diagrams. A simplified version of a functional model for the filter design in Figure 3a is illustrated in Figure 4 below.

One of the things this type of diagram is commonly used to do is to act as a focus for thinking about ‘trimming’ (‘pruning’, ‘simplification’, or whatever other word we wish to use) the system. This is the tool we use to provide provocations that encourage us to reduce the partcount within a system. One of the provocation questions we might apply, for example, when looking to simplify this filter design, would be ‘let’s eliminate the back-flush nozzle’. As soon as we make this provocation, we have identified a problem because if that component is eliminated then there is nothing in the system that is now delivering the useful function ‘cleans filter’ – Figure 5.

This is the point at which we ask the standard ‘trimming’ questions:-

– Do I need the function offered by the part?
– Can something else in or around the system perform the function?
– Can an existing resource perform the function?
– Can a low cost alternative perform the function?
– Must the part move relative to other parts
– Must the part be of a different material or isolated from its mating parts?
– Must the part be separate from mating parts to facilitate assembly or dis-assembly

Typically, we will ask these questions in a top-down sequence. If we get to the second question (i.e. if we decide that we do require the function that the trimmed component once delivered), and we are looking to the remaining components in the system to see if they can perform the function, what the ‘self’ aspect of TRIZ is trying to get us to think about is ‘could the filter ‘itself’ deliver the function. We can represent this question pictorially as shown in Figure 6.

This ‘can I get the component to deliver the function by itself?’ question, then, is a key ideality driver. It is not always so obvious in when we are looking at the trimming questions, but as the ‘self’ concept suggests, the component ‘itself’ is a possibility we should always examine when using the trimming tool.

‘Self-X Patents’
A study of ‘self’-based patents (including the synonyms of ‘self’ – ‘automatic’, ‘auto-‘, etc) on the US patent database has been conducted in order to establish the state of the art in terms of what functions the world knows how to get systems to deliver ‘by themselves’. The searches were done using the Boolean text facilities found at www.delphion.com, and covered the period from 1985 to 2001. The bulk of the study focused on an examination of what sort of things it is that inventors are getting their inventions to do by themselves.

Figure 7 illustrates the resulting breakdown. Over 2000 patents have been studied on a case-by-case basis in compiling the figures. It has not been possible to discriminate absolutely between ‘traditional’ and ‘ideality-driven’ solutions, but, rather, the point has been to examine the functions that inventors have been trying to get their inventions to deliver. The data is presented in descending order of frequency, such that ‘self-aligning’ is the most frequently occurring ‘self-X’ patent type.

The figure highlights a number of interesting points. Firstly, while there may be some debate over the inclusion of the ‘self-contained’ category – which doesn’t necessarily contain a function – it is interesting to note that ‘self-contained’ occurs significantly less frequently than the most common ‘self’ function, ‘aligning’. There are in fact close to 200 patents focused on delivering a ‘self-aligning’ capability.

‘Self-aligning’ may be seen as a whole family of similar patents (adjusting, positioning, centring, levelling, opening/closing, etc) associated with a physical movement. In just about all cases, the degrees of movement being achieved are relatively small. This is perhaps significant in terms of defining the state of the art – several inventors know how to make physical things move themselves, just not very far.

Another big class of ‘self-X’ functions is then concerned with the delivery of (relatively easy to obtain) non-physical changes. Such functions primarily consist of measurement-based functions such as ‘self-test’ and ‘self-time’ (many computer applications), or, on the mechanical side, ‘self-regulate’, ‘self-limit’, or ‘self-calibrate’.

Moving down to the less frequent applications then are inventions which make use of new and emerging scientific knowledge. This category includes, for example, things that expand or contract by making use of shape-memory alloys or polymers, things that clean themselves using the Lotus Effect or photo-catalytic elements, things that heat themselves using a sodium acetate (or similar) phase transition energy storage means, things that self-learn as a result of increasing use of genetic algorithms and expert systems in computing, and so on.
A final group of ‘self-X’ types – self-balance, self-seal, self-repair, for example – represent relatively recent innovations which have not as yet reached the eyes of the majority of problem solvers. Self-balancing things are particularly interesting in this context. Just about any industry that designs things that rotate faces a balance issue at some stage – either during manufacture (where we set tight tolerances in order to reduce out of balance forces) or assembly, or test (most sectors invest significantly in machinery to facilitate balance operations), or in service (where out-of-balance forces are a major contributor to nonreliability of systems of all descriptions). Few, if any, on the other hand appear to have recognised the existence of several, highly amenable to transfer to other industry sectors, good patents in this area. This is a topic we will return to in the second article in this series. The ‘others’ category includes a wide range of ‘self-X’ functions with only one or two references. These include functions like mold, sinter, polish, illuminate, deodorise (!), which again represent capabilities (or potential capabilities) that have thus far not been widely exploited by other problem solvers.

‘Self’ and Your Problem
Solutions that achieve functions ‘by themselves’ are very important in the sense of a world in which the overall technology evolution driver is increasing ideality.

In this sense, the concept of Ideal Final Result, and the idea of looking for solutions which incorporate the word ‘self’ – i.e. the problem solves itself – is a very powerful tool in the TRIZ armoury.

Some problems contain constraints which make it difficult if not impractical for the problem owner to consider using the IFR method, but that being said, the schema illustrated in Figure 8 (Reference 1) is a useful start point for a good number of problems. Ideal Final Result thinking encourages problem owners to first register the function that they are wishing to deliver, and then gets them to think about how the system could deliver that function by itself – i.e. without the addition of the increased complexity inherent to traditional problem solving methods.

The ‘self-X’ solutions of others to be found on the patent database are testament enough to the fact then that someone may already have successfully achieved the ‘self’ delivery of a function we wish to achieve ourselves.

Conclusions
1) ‘Self’ is a very important word in the context of looking for good solutions to problems; if a system can solve a problem ‘by itself’, it will be a more ideal solution than one that requires the inclusion of external factors which serve to complicate the system.
2) There is a difference between traditional and ideality-driven definitions of ‘self’. Traditionally, if we add new functions, the system has to become more complex. The ideality-driven definition gets us to think harder about whether we can achieve the additional functionality using resources that already exist in or around the system, and without increased complexity.
3) The patent database provides a good start point (knowledge resource) for highlighting the sorts of ‘self-X’ functions being achieved by other problem solvers. Next month, we will shift our attention to some specific examples of ‘self-x’ inventions and at the general lessons we ought to learn from them.

References
1) Mann, D.L., ‘Hands-On Systematic Innovation’, CREAX Press, April 2002.
2) Domb, E., ‘Using the Ideal Final Result to Define the Problem to Be Solved’ TRIZ Journal, June 1998.
3) Belski, I., ‘I Wish The Work To Be Completed By Itself, Without My Involvement: The Method Of The Ideal Result In Engineering Problem Solving’, TRIZ Journal, April 2000.