Editor | On 10, Feb 1999

Re-printed from the TPD Symposium.

Semyon D. Savransky, Ph.D.
The TRIZ Experts, USA
E-mail: TRIZ_SDS@Hotmail.com

1. Introduction

The polyscreen approach proposed by Genrich Saulovich Altshuller is used in this paper to discuss a possibility of superconductivity in chalcogenide glasses and even their melts* at sub-screen, some general ideas in superconductivity at the main screen, and basic features of doing science at the super-screen. The goals of such approach are to involve scientists into TRIZ paradigm, to demonstrate TRIZniks the culture of natural sciences, and to present peculiarities of semiconductor-superconductor transitions.

Figure 1. The polyscreen presentation of some research in superconductivity

The polyscreen approach (sometimes called as the system operator) allows TRIZniks to compare and predict different stages of evolution of a technical system. Here it is used for estimation of critical temperatures of the transition into superconductivity state Tc and development of physics (see the figure 1). To the best of the author knowledge, it is the first attempt to present results of TRIZ (and even scientific research) in such form.

* Chalcogenide glasses are the wide class of amorphous semiconductors on the base of elements of VI group of the Mendeleev’s periodic system, e.g., As-S-Se
alloys.

2. The Super-Screen: SCIENCE

As it is known, the lists of physical, chemical, etc. effects for design of new devices and creation of new technologies is the important part of TRIZ [1,2] . However, TRIZ is very rarely used in purely academic investigations [3] yet and, as far as we know, there were no attempts to exploit the TRIZ ideas for revealing the new forms of matter earlier. (It should be noted that investigations of this type are very rare in scientific practice and their results are compatible with inventions of the 5^thlevel [1,2] in engineering).

Continuity is inherent in most scientific investigations. By continuity is meant here the perfect authors’ knowledge of results of previous investigations and state of a problem. By the way, that is why the exchange of preprints (papers before their publication) between scientists is universally accepted in intensively developed branches of science. This exchange significantly catalyzes the scientific research and creates the benevolent working atmosphere in association of professionals. Unfortunately, we lost such milieu in TRIZ in few last years.

Physicist from different countries have participated in the research presented in this paper – development of superconductors. Although all participants (except the author) were not familiar with TRIZ at the time of research discussed in this paper, they often intuitively used some TRIZ ideas. The author of this paper, who thoroughly has studied all TRIZ literature in 1980-1981 and continuously keeps track of modern publications, believes that he applies the TRIZ technique at the level of well inoculated conditioned reflex now. It is simple to track that such TRIZ concepts as the
ideality, sub-systems and resolution of physical contradictions have been used in the research of superconductivity in non-crystalline materials performed by the author during last 15 years (some results are presented an the sub-screen).

References to the super-screen

1. G.S. Altshuller “To Find an Idea” (Novosibirsk, Nauka, 1991)
2. S. D. Savransky, “TRIZ” 1999, 454 pp.

3. G.S. Altshuller, In Solution of Research Problems (Kishinev,
   1991).

3. The Main Screen: SUPERCONDUCTIVITY

Heike Kamerling Onnes, a physicist from Netherlands, discovered superconductivity (capability of a material to conduct electricity without resistance) in mercury cooled by rare and expensive helium below the critical temperature (Tc) 4.2 K in 1911. In spite of discovery of superconductivity in many other materials, the fundamental theory of their behavior /BCS theory/ was published by the American physicists John Bardeen, Leon N. Cooper, and J. Robert Schrieffer only in 1957 (see, e.g. [1,2] ) .

The BCS theory is based on the attracting interaction between electrons, which takes place due to their interaction with phonons /quantum atomic vibrations that propagate through the whole crystal lattice of a solid body/. In low-temperature superconductors, these quasi-particles (electrons + vibrations) hinder phonons to spread such couples and create the force, which overcomes the inter-electron repulsion. This Cooper’s coupling in the momentum space can occur only when the
temperature T is sufficiently low, so that usual thermal motion of electrons is diminished. Cooper’s couples avoid collisions resulting in usual resistance. Electrons have spin equal to 1/2, however their couples will have spin equal to 0 or 1. This creates prerequisite to their condensation and superfluid in coherent state. Since the electron pairs carry the electric charge, their superfluidity will be automatically accompanied with superconductivity just at their formation at some Tc named the critical temperature of superconductivity transition.

For almost 30 years after creation of the BCS theory, efforts of thousands physicists and materials scientist built up the Tc value only up to 23 K in metal alloys, that caused crisis in the research. The BCS theory describes low-temperature superconductivity in metals and cannot show ways to increase Tc strongly. Nevertheless, some applications of the low-temperature superconductors have been developed, such as, for example, high-power magnets, SQUID detectors, devices for image formation (MRI), etc. Due to high cost (about $10 for gallon) and inconvenience of helium cooling needed to keep materials in superconductivity state, these and other applications of low-temperature superconductors were not considered as economical for wide commercial usage [3] .

It becomes clear that high-temperature superconductors must be sought for beyond the mechanism of BCS theory, hence number of models have been proposed [1,2] . One of the most promises ideas is the theory of superconductivity related to the Bose-Einstein condensation of local pairs in the coordinate space [4,5] . Such condensation of quantum particles with integral spin was considered more than 70 years ago by the Indian physicist Satyendra Nath Bose and the German (at that time) theorists Albert Einstein.

Significantly simplifying the situation, we can compare the Bose-Einstein condensation with gas transition into liquid. Such transition takes place either at temperature decrease (and consequent decrease of gas kinetic energy) or at pressure increase (and consequent decrease in distance between gas molecules).

This new state of a matter was discovered in liquid helium at its transition into the superfluid state. Experiments of the Soviet physicist Pyotr Leonidovich Kapitza in Great Britain and the American physicists Robert C. Richardson and David M. Lee in 1938 and 1971 have shown that superfluid property is inherent in both isotopes of helium. The detailed pattern of this phenomenon was developed by the Soviet theorists Lev Davidovich Landau.

Here our story transforms from the consequent in time to the parallel one as it usual for polyscreen approach in TRIZ. At this stage, barriers between different disciplines in physics had an adverse effect on science development because the specialists in superconductivity and glasses did NOT know works of each other. The abundance of information about the results of research in natural sciences are published in many journals in different languages (although, in the case under consideration, the papers were published in the most readable Soviet and American physical journals) that make hard to a researcher to find appropriate result from another (even close) field. On the author’s opinion, the modern Internet WWW technology as well as the detailed and expanded TRIZ lists of effects can improve this situation. So, let us describe briefly the decade preceding the discovery of so-called high-temperature superconductivity.

The American and Great Britain theorists Philip W. Anderson and Nevill F. Mott together with the American physicist Robert A. Street considered the possibility of existence of local electron pairs in chalcogenide glasses in 1975 [6,7] . This theory was experimentally justified by three research groups [8] in 1982-1985. In 1983-1984, the author of this paper hypothesized that superconductivity is possible in chalcogenide glasses alloyed with some transition metals with d-shell, which can increase the concentration of the local electron pairs in these glasses [9] . It should be noted that a year earlier the model of superconductivity at the expense of local pairs was independently developed by the Soviet theorists I.O.Kulik, A.G. Pedan (Kharkov, now Turkey), A.S. Alexandrov (Moscow, now Great Britain), and the French physicist J. Ranninger [10] . Initially the authors of Ref. 10 did not know about existence of the chalcogenide glasses at all, while S.D. Savransky (Novgorod, now USA) had no deal with superconductivity and did not know about Ref.10 and the whole idea of local pairs superconductivity. Few days later after the appearance of the hypothesis about superconductivity due to the local pairs in chalcogenide glasses, the experiments were performed by I. V. Berman and N. B. Brandt (Moscow State University) with V. I. Sidorov (AN Institute of High Pressure Physics), in which the superconductivity at high pressure Pin these materials was discovered [11a] . The first experiment was performed with the glass Ge33As12Se55untypical for academic research but widely used for submarine windows in USSR Navy, then more simple structures have been studied [11 b,c] .

The idea of local pairs superconductivity was taken into consideration during studies of ceramics in IBM research division in Switzerland. In April 1986 K. Alex Muller and George Bednorz discovered superconductivity in the ceramic La2-xBaxCuO4 at 35 K, which becomes the first high-temperature superconductor [3] . During the tests of this sensation result it was found that Tc increases aspressure P grows. This fact leaded the group of physicist from the University of Houston (USA) to the TRIZ conclusion – instead to increase Tc from outside, some atoms should be injected into the material that press the structure from the inside (i.e. TRIZ system convolution into substance). Already to the late of 1986, this group headed by Paul C. W. Chu overcame the so-called nitrogen limit (the temperature of liquefying of readily available and inexpensive nitrogen) at the expense of injection of metals with d-shell into the material. The Houston group in co-operation with the Chinese physicist M. K. Wu reached the stable and reproducible superconductivity with Tc close to 100 K in Y1Ba2Cu3O7-din January 1987 [3] . Time regularity of increase in the temperature Tc looks like the S-shaped curve well-known in TRIZ with the values 110 K and 125 K for bismuth cuprates found in 1988 up to the record Tc = 164 K discovered in mercury compounds under pressure in 1993 and further stop in Tc growth at the level more than 100 K below than the room T ~300 K [3] . In all cases, superconductivity is caused by alloying of initial matrix of Cu and O atoms resulting in change of the electron spectrum.

It should be noted that several technical comprehension of this so-called high-temperature superconductivity only arises recently, and many nice applications of this phenomena are yet not found. But again, Tc is still too small for industry.

The attack to the problem of the high-temperature superconductivity is unprecedented over the whole history of science. Now several hundred of physical, chemical, and materials research laboratories all over the world are involved in the studies of the high-temperature superconductivity in ceramics and similar crystals. The questions arise:

– does the curve of growth in the temperature of transition into the superconductor state Tc reach its saturation for cuprate materials ? and

– is there the necessity to pass to other S-shaped curve (i.e., to a new class of material) or the period during which the cuprate materials are studied is too short and new discoveries can be done in this direction?

The author does not undertake to solve these problem and simply calls attention to unusual regularities of the transition into superconductor state in the chalcogenide glasses, to the record Tc for sulphur (the highest superconductor transition temperature have been observed in the single-element materials), and to strange semiconductor-metal transformation in chalcogenide melts e.g., in selenium [9,11-15] . These results are presented at the figure 2.

Figure 2a. Pressure dependence of Tc in sulphur obtained by Russian, American and Chinese researchers [14e] .

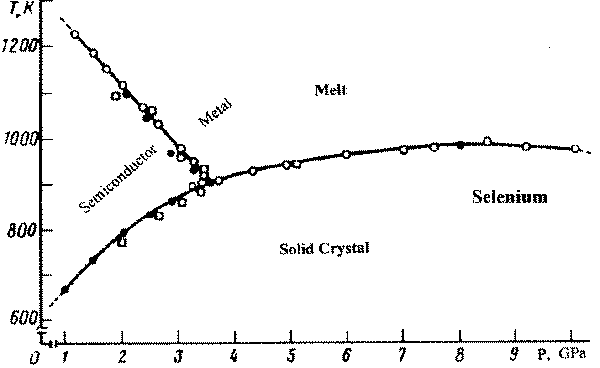
Figure 2b. Pressure dependencies for Se [14a] .

The explanation of these results and some details of superconductivity in selenium are discussed in the next sub-screen. The reader who is not interested in condensed matter physics can skip this part.

References to the main screen

1. M. Tinkham, “Introduction to Superconductivity.” (McGraw Hill, 1995).

2. D.R. Tilley and J. Tilley, “Superfluidity and Superconductivity.” (Adam Hilger Ltd, 1990).

3. G. Vidali, “Superconductivity : The Next Revolution?” (Cambridge Univ. Press, 1993)

4. A.A. Abrikosov, “Fundamentals of the Theory of Metals” ( North-Holland, 1988).

5. A. S. Alexandrov and N. F. Mott “High Temperature Superconductors and Other Superfluids” (Taylor & Francis, 1995)

6. P.W. Anderson, Phys. Rev. Lett. 34 (1975) 953.

7. N.F. Mott and R.A. Street, Phys. Rev. Lett. 35 (1975) 1293.

8a. D.L Fox., B. Golding and W. Haemmerle, Phys. Rev. Lett. 49 (1982)
1356.

8b. T.Thio, D. Monroe and M. Kastner, Phys. Rev. Lett. 52 (1984) 667.

8c. Z. Vardeny and J. Tauc, Phys. Rev. Lett. 54 (1985) 1844.

9. S.D. Savransky, Low Temperature Physics 23 v.1 (Tallinn, 1984) 217.

10?. I.O. Kulik and A. G. Pedan, JETF 79 (1980) 1469.

10b. A.S. Alexandrov, J. Ranninger, Phys. Rev. B. 23 (1981) 1796.

10c. R. Micnas, J. Ranninger and S. Robaszkiewicz, Rev. Mod. Phys. 62 (1990) 113.

11?. I.V. Berman, N.B. Brandt, V. A. Alekseev, I. E. Kostyleva V.I. Sidorov, and O.P. Pyatkina, JETF Lett. 40 (1984) 472.

11b. I.V. Berman and N.B. Brandt, Low Temperature Physics 16 (1990) 1227 .

11c. V.A. Alekseev, I.V. Berman and V.I. Sidorov, Zeitsc. fur Phys. Chem. Bd.156 (1988) 271.

12a. S.D. Savransky, J. Non-Crystal. Solids 83 (1986) 235.

12b. S.D. Savransky, J. Non-Crystal. Solids 94 (1987) 412.

12c. S.D. Savransky, Solid State Communications 79 (1991) 843.

12d. S.D. Savransky, Materials Science and Engineering A145 (1991) 109.

12e. S.D. Savransky, Mater. Res. Bull. 28 (1993) 81.

12f. S.D. Savransky, J. Non-Crystal. Solids 164-166 (1993) 1173.

12g. S.D. Savransky, Physical Review B 52 (1995) 7434.

12h. S.D. Savransky, High Temperatures – High Pressures 27 (1996) 377.

12i. S.D. Savransky, In Impact of Recent Advances in Processing of Ceramic Superconductors (1998) 231.

13a. S.A. Dembovsky and E.A. Chechetkina “Glass Formation” (Moscow, Nauka. 1990).

13b. M.I. Klinger, Phys. Repts. 165 (1988) 275.

13?. S.D. Savransky, In The Hubbard Model: Its Physics and Mathematical Physics. Eds.: D. Baeriswyl, D.K. Campbell, J.M.P. Carnelo, F. Gunia and E. Louis; NATO ARW Proceedings (Plenum Press, New York, 1995).

13d.S.D. Savransky, In Defect- and Impurity-Engineered Semiconductors and Devices. Eds.: S. Ashok, J. Chevallier, I. Akasaki, N.M. Johnson and B.L. Sopori; MRS Proceedings 1995, v. 378.

13e. S.D. Savransky, Philosophical Magazine Letters 66 (1992) 91.

13f. S.D. Savransky,Hopping and Related Phenomena 5 (1994) 117.

14a. V.V. Brazhkin, Voloshin R.N. and Popova S.V., JETF Lett. 50 (1989) 424.

14b. G.N. Stepanov and E.N. Yakovlev, Materials Research Soc. Sump. Proc. 22 (1984) 127

14c. K. Tamura,J. Non-Cryst. Solids 117/118 (1990) 450.

14d. Akahama Y., Kobayashi M. and H. Kawamura, Solid State Communications, 84 (1992 ) 803.

14e. V.V. Struzhkin, R.J. Hemley, Ho-kwang Mao and Y.A. Timofeev, Nature, 390 (1997) November 27 issue.

15. S.D. Savransky, Unpublished results 1995-1998.

4. The Sub-Screen: SUPERCONDUCTIVITY IN AMORPHOUS AND LIQUID SELENIUM

The features of superconducting transition (ST) in the amorphous selenium (a-Se) [1-5] and other chalcogenide glasses [6,7] that occurs at high pressures P at low temperatures T cannot be explained by the BCS theory, but describes well by the local pairs’ theory of superconductivity [8,9] .

The existence of local pairs (LP) in disordered Se well fixed [10] . In the liquid selenium (l-Se) LP create at the chains’ ends [10-15] with energyE = 0.14 eVper electron [15] . Let discuss from this point of view experiments shown at the figures 1 and 2.

LP are frozen in a-Se with the concentration N ^~1019 cm-3 because the typical chain consists of L = 104-105 atoms [10-14,16] . LP pin the Fermi level F near middle of the gap Eg and LP binding energy Eb»
Eg [10, 15] . Eg reduces from 2.05 eV to 0 in l-Se from the melting point Tm to the semiconductor – metal transition at Tt» 1600K then P ³0.5 kbar [14, 17] , and dTm/dP³10 grad/kbar in Se [16] . In the linear approximation used here a value dEg(l)/dT»10-3 eV/grad in l-Se that is only 10% of dEg(a)/dP in a-Se [17-19] . The chain structure of l-Se destroys at Tt but the two-fold coordination structure is preserved below and above the semiconductor – metal transition in l-Se [17-20] . The l-Se again returns to an insulating state in the immediate vicinity of the critical point Tcr in another structural state [17] . The semiconductor – metal transition shifts to lower T under grown P in l-Se (dTt/dP»100 grad/kbar near 1500 K) [11-14] . The semiconductor – metal transition occurs in a-Se under high P > 70-100 kbar [1-5,19] when F shifts to the mobility edge Em [3,21] . Since L reduces in l-Se from ~ 104 atoms at Tm to L = 7-10 atoms near Tt [14,17] , so N strongly increases above 900 K up to NA/L ~ 6.1022 cm-3 at Tt (NA is the Avogadro number). Spin density is 0.1.NA/L at Tt [14] , hence LP exist at this T.

In the local pairs’ theory of superconductivity [8,14] the temperature Tc and width dTc of ST is coupled with the Bose-Einstein condensation of LP with mass M as:

Tc ^~ N2/3/M, dTc/Tc ^~ N4/3.

Hence, LP band-width t is:

t ^~ M1/2(Tc3dTc)1/4lnM.

The parameters of a-Se have been determined [21] on the basis of the most detailed data [5] . The concentration N is about (1-3).1019 cm-3 at P < 130 kbar, i.e., all LP taking part in ST, because P destroys Se chains. Mass M lies in range (4-8).m
at P = 100-110 kbar, m is the free electron mass. Band t is relatively wide »1-10 meV in a-Se at same P [21] .

The kinetic mass of LP at the normal P estimated from M values is ~ 800m in a-Se. All characteristics of ST in a-Se correspond to predictions of the local pairs’ theory of superconductivity [21] . With these facts in mind let us show that l-Se can be the local pairs superconductor.

For the Arrhenius activation N = NAexp(-E/T) the simple equation

Tc = k.[exp(- E/Tc)] 2/3/M

describes the ST temperature in a liquid there LP create, and k = 4.28.104.

P, kBar

T, K Figure 3. The P – T diagram for l-Se [21,22] . The superconducting regions could exist in white area around actual to. Note the similarity of the theoretical predictions with the experiment results (fig.2).

The numerical solution [21,22] shows that T-M line separates a region of possible superconducting state from a region with normal state for P discussed below. ST could begins from Tl ~ 900 K and ends at Tt for actual M and N. LP unstable at very high T, so region of ST could ends at Tu = Eg which is ~ 1500 K in l-Se. Since l-Se is asemiconductor near Tl, it is necessary to apply P that shifts F to Em i.e., to the state nearby to the semiconductor – metal transition then t »|F-Em| [21] , but not deep into a metallic state where LP are destroyed in l-Se. Hence, the lower and upper pressure’s limits are estimated as:

Pl=[Eg(Tc)-t] /[dEg(l)/dP] ,

Pu = Pl + Tc[dTt/dP] -1.

The P – T diagram for l-Se is shown at the figure 3 for the actual values t ~ (0.2 – 1.6)* Tc. The white superconducting region is limited by Pl and Pu, Tu and Tl the boundary solid – liquid metal at T ~ 1050 – 1120 K, so for actual t the necessary P lie below 60 kbar in superconducting l-Se. The lines that are shown for different to =t/Tc values indicate the low T and high P limits in this region for ST due to LP.

Another possibility to increase of N is connected with destruction of Se chains by impurities (e.g., Te, As, K, Cl). Moreover, some impurities can create own LP in a- and l-Se [10] . Then the distance between neighbor LP decreases, so t increases and M decreases. Probably the conditions for ST can be softened in l-Se doped by these elements, and in other melts of chalcogenide glasses with small energy E.

Note that conditions for ST in l-Se are found in the linear extrapolations of the dependencies are known ordinarily in the range 0.5-2 kbar to higher P (see, however,[20] ). More correct approximations shift numerical values of parameters, but probably do not change the main conclusion that LP superconductivity is possible in liquid Selenium and some other liquid chalcogenide alloys at high pressures.

References to the sub-screen

1. J. Witting, Phys. Rev. Lett. 15 (1965) 159.
2. A.R. Moodenbaugh, C.T. Wu and R. Viswanathan, Solid State Commun. 13 (1973) 1413.
3. F.P. Bundy and K.J. Dunn, Phys. Review B22 (1980) 3157.
4. Y.Akahama, M. Kobayashi and H. Kawamura, Solid St. Commun. 84 (1992) 803.
5. M.A. Il’ina, Sov. Phys. Solid State 26 (1984) 5747.
6. I.V. Berman, N.B. Brandt, Soviet Phys. J. Low Temp. Phys. 16 (1990) 1227.
7. S.D. Savransky, Solid St. Commun. 79 (1991) 843.
8. R. Micnas, J. Ranninger and S. Robaszkiewicz, Rev. Mod. Physics 62 (1990) 113.
9. A.S. Alexandrov and N.F Mott, Rep. Progr. Phys. 57 (1994) 1197.
10. N.F Mott and E.A. Davis, Electronic Processes in Non-Crystalline Materials,
    Oxford (1979).
11. M. Culter, Liquid Semiconductors. New York, 1977.
12. A.R. Regel and V.M. Glazov, Principles of Structure Formation of Electronic Melts. Moscow, 1982.
13. J.E. Enderby and A.C. Barnes, Repts. Progr. Phys. 53 (1990) 85.
14. W.W. Waren (Jr.) and K. Dupree, Phys. Rev. B22 (1980) 2257.
15. L.F. Gladden and S.R. Elliot, J. Non-Crystal. Solids 97/98 (1987) 1175.
16. P.J. Ford, G.A. Saunders, E.F. Lambson and G. Carini, Physica Scripta 37 (1987) 894.
17. K. Tamura,J. Non-Cryst. Solids 117/118 (1990) 450.
18. K. Tanaka, Disorderd Systems and New Materials. (1988) 290.; Phys. Review B42 (1990) 11245.
19. G. Parthasarathy and E.S.R. Gopal, Bull. Mater. Sci., 7 (1985) 271.
20. V.V. Brazhkin, R.N. Voloshin amd S.V. Popova, JETF Lett. 50 (1989) 424.
21. S.D. Savransky, High Temperatures – High Pressures 27 (1996) 377.
22. S.D. Savransky, Impact of Recent Advances in Processing of Ceramic Superconductors
    (1998) 231.

5. Conclusion

The possibility of existence of a new form of matter – liquid high-temperature superconductors in melts of chalcogenide glasses – is predicted. Undoubtedly, the liquid high-temperature superconductors will give rise to many inventions, for example, in magneto-hydrodynamic propulsive agents.

It is also shown that openess of researches from different countries leads to progress in science. Many names mentioned above were awarded with Nobel prize (Heike Kamerling Onnes, John Bardeen, Leon N. Cooper, J. Robert Schrieffer, Satyendra Nath Bose, Albert Einstein, Pyotr Kapitza, Lev Davidovich Landau, Philip W. Anderson, Nevill F. Mott, K. Alex Muller and George Bednorz). Nobel prize “waits” also for a scientist, who will be successful in explanation of superconductivity in Y₁Ba₂Cu₃O_7-d
and other cuprates, as well as the one who will find the superconductivity at temperature above the room one. Although thousands of papers are published about the high-temperature superconductivity, the mechanism of this phenomenon is still unclear. Maybe the reason is that physicists, chemists, and specialists in materials do not know TRIZ (?).

In conclusion, the author would like to note again that the open information exchange between scientists from different countries and continents is actual for TRIZ now in order to become a genuine science.

About the author:

Semyon D. Savransky, a member of the International TRIZ Association, became acquainted with TRIZ in 1980-1981. Now Semyon D. Savransky is one of the distinguished TRIZ experts who combines his experience in engineering, science and pedagogic. He has applied TRIZ for several R & D projects in various high-tech industries in Russia and USA. Semyon D. Savransky is the author of about 150 patents and scientific papers in physics, TRIZ, materials science, electronics, and optics. He received his Ph.D. in 1989 in Leningrad /St. Petersburg now /, and his academic background
is split between Novgorod State University (Russia), University Pais Vasco (Spain) and New York City University (USA). Currently Semyon D. Savransky is the head of the R&D Division of West Coast Quartz Corporation (California). He is the founder of the Research Center in Novgorod State University – NGPI (Russia) and The TRIZ Experts International Company.