Editor | On 18, Mar 2005

Toru Nakagawa
Osaka Gakuin University, Japan
e-mail: nakagawa@utc.osaka-gu.ac.jp

Abstract
The biggest reason for slow penetration of TRIZ into industries in Western countries is that very rich contents of TRIZ knowledge bases and individual methods of problem solving have been tried to teach without clear overall procedure/structure for problem solving. It has been traditional that principal solution generation methods in TRIZ, including Inventive Principles, Inventive Standards, and Trends of Evolution, are applied separately on the basis of their own problem analysis methods. Present paper demonstrates, on the other hand, that Unified Structured Inventive Thinking (USIT) is a simplified and unified version of TRIZ which has overcome the above-mentioned weak-point.

All the solution generation methods in TRIZ have been reorganized into a unified hierarchical system of USIT Solution Generation Operators. On this basis, USIT has a clear procedure for creative problem solving process as shown in a flowchart and also has a clear structure, as shown in a dataflow diagram, of transforming problem information stepwise into solution information.
User’s specific but vague problem is (1) first converted into a ‘well defined problem’ at the problem definition phase, then (2) further converted into the understanding of the problem system in terms of objects, attributes, functions, space, time, ideal actions, and ideal properties at the problem analysis phase, (3) modified by applying the USIT Operators into pieces of ideas of a new system in the solution generation phase, (4) constructed into conceptual solutions on the basis of user’s technological background capabilities, and (5) finally implemented into user’s specific solution(s) in the implementation phase. USIT guides at the steps (1) through (4). USIT has been taught fully in 2-day training seminars at the level of solving real industrial problems by the participants themselves.

1. Introduction
Theory of Inventive Problem Solving (TRIZ) [1, 7, 9, 2] is a powerful methodology for creatively solving problems in a wide range of technological (and many other non-technological) fields. It has established knowledge bases (KBs) of technological facts with various useful indexing systems and of principles for inventive thinking and has also developed a large number of methods for problem definition, problem analysis, and solution generation. These KBs have been constructed by extracting world best solutions in science and technology, and the problem solving principles in TRIZ are at a high level of abstraction so as to be applicable to a wide range of problems.
In spite of expectations by TRIZ experts, however, TRIZ has not been spreading so widely and rapidly in the Western countries since its exposure in early 1990s. The present author [3] observes, as many would agree, that the penetration of TRIZ has been slow not because it is poor but because it is so rich in contents. ‘How to choose an effective principle’ and ‘how to apply a principle properly to the user’s specific problem’ have been the issues for TRIZ users. Most TRIZ specialists have tried to teach the rich contents of TRIZ KBs and thinking methods in more or less orthodox forms, but most engineers in industries and engineering students cannot understand them up to the level being able to apply them to their real problems. Some specialists may say ‘It is a problem of the students and the training period’, but the position of the present author in this paper is ‘It is a problem of the teachers and the system of TRIZ itself.’

Basic model and overall structure of TRIZ should be reviewed and discussed in this context. It is generally understood that TRIZ is based on the four-box scheme of problem solving [2] shown in Fig.
1. Instead of trying to solve user’s specific problem directly to specific solutions staying at the concrete level, TRIZ advises to go around at a higher abstraction level using standard models which show generalized problems and their generalized solutions. TRIZ has adopted this scheme from the sound basis of science and technology.

Fig. 1 Four-box scheme of problem solving
All the TRIZ KBs (such as Effect database, Inventive Principles, Inventive Standards, Trends of Evolution, etc.) have been built with the intention to let them serve as different models at the abstract level in this scheme.

Once models are established, the process of problem solving may be reduced to the following issues:
• Abstraction: How can we transfer the specific problem to the generalized problem in some known model? Do we need different abstraction methods for different models?
• Selection: Which model should we use among a number of models?
• Concretization: How can we transfer the generalized solution suggested by the model to a specific solution to our problem?
Generally speaking, these issues are not well understood unfortunately in many fields of science and technology.
In each topic of a specialty field, one model is chosen and taught with a few examples.
Then the students have to learn, study, drill and practice many times to understand by themselves that the model is useful for some kind of problems after some kind of abstraction. TRIZ has developed a number of procedural methods of problem solving in technology, for the purpose of guiding us in the abstraction and selection (and little in the concretization) processes. These methods in TRIZ (such as 9-Window Method, Substance-Field Analysis, Technical and Physical Contradictions, etc.) are often very unique and powerful in the areas where no other effective methods and ways of thinking exist. Nevertheless, the overall procedure of problem solving in TRIZ has not been well established yet and is in a confusing situation for users.
In the present paper, the current situation of the TRIZ methodology is summarized briefly in this four-box scheme. Then I will demonstrate that Unified Structured Inventive Thinking (USIT) [8] , i.e. a simplified and unified version of TRIZ, has established a clear structure of problem solving procedure by extending the four-box scheme into more meaningful six-box scheme. The key to this structure is the USIT Solution Generation Operators, which have been obtained earlier by reorganizing all the TRIZ principles and methods for solution generation [4, 5] .

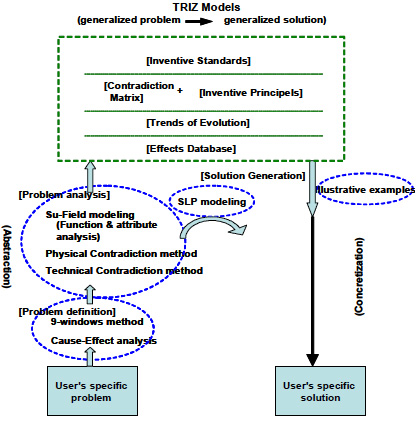
2. Current Scheme of Problem Solving in TRIZ
The current situation of the overall scheme of problem solving in TRIZ may be roughly
summarized as shown in Figure 2 in the framework of Figure1. TRIZ KBs are shown in a box at the
top and various TRIZ methods are shown in ovals according to the phases in problem solving. These
components are established well [1, 7, 9, 2] and are summarized in the following subsections first and
the overall structure will be discussed next.

Figure 2. Overall Structure of Problem Solving in Traditional TRIZ

2.1 TRIZ Knowledge Bases of Principles and Facts
First type of KBs in TRIZ is the accumulation of facts and technical means, especially:
• Effects Database: facts database of physical, chemical, and mathematical effects and technical means
This type of KB is useful to learn various facts and means known in different fields of science and technology and to apply them to our own fields in novel ways. Reorganizing the KB in the explicit hierarchical system of functions has been a major contribution of TRIZ.

Second type of KBs in TRIZ is at a higher level of abstraction of the principles for inventive thinking and has been the most important contribution of TRIZ. They include:
• 40 Inventive Principles: essence of ideas in inventions
• Contradiction Matrix: information of which Inventive Principles have been most frequently used in which type of problem expressed in the Technical Contradictions
• 76 Inventive Standards: standard solutions corresponding to the situations expressed by the Substance-Field model
• Trends of Evolution of Technical Systems: patterns of evolution

These are the major models in TRIZ in the four-box scheme and provide problem solvers with generalized solutions for generalized problems. For each item in these KBs, examples of typical cases of application are accumulated and linked (e.g., to the Effects Database and to patent databases) and used for illustrating and stimulating users’ analogical thinking. It should be noted that these KBs are presented to users as parallel alternatives, separated (and more or less overlapped) with one another, as shown with the separating broken lines in Figure 2.

2.2 Individual Methods and Techniques for Problem Solving in TRIZ
In the area of methods and techniques for problem solving in technology, Classical TRIZ has developed a number of unique and effective methods. Major ones are summarized below briefly with particular comments on their relationships to the TRIZ KBs:
• 9-windows method: to think over the problem in the 3 x 3 framework of system hierarchy (i.e., super-system, system, and subsystem) and time (i.e., past, present, and future). This is a general method to be used in the early stages of problem definition and problem analysis. It is loosely related to the usage of the KB of Trends of Evolution.
• Substance-Field modeling: to model the problem system with two substances (i.e., product and tool) and its functional relationship. This serves as the problem analysis procedure (i.e. an abstraction process) for using the KB of Inventive Standards.
• Technical Contradiction method: to model the problem in the scheme of a Technical Contradiction where the problem solver wants to improve one aspect (or parameter) of the system but another aspect of the system gets worth and preventing the improvement. This is a special method in the abstraction process for using the Contradiction Matrix (in the selection process) and then a few selected Inventive Principles.
• Physical Contradiction method: to model the problem in the scheme of a Physical Contradiction where two opposite requests exist simultaneously on one aspect of the system, and then to use the Strategy of Separation of the opposite requests. This strategy guides the solver to several selected Inventive Principles.
• Smart Little People’s modeling: to imagine that a part of the system is composed of a crowd of smart little people who can and do perform any desirable action. This method stimulates to think of ideal solutions first and then to figure out solutions in feasible, technical terms. It does not utilize any KBs.

Recent works in TRIZ have added some more methods, including:
• Cause-Effect analysis: to model a network of cause-and-effect relationships in the problem, and to suggest a large number of smaller and more specific problems of preventing some harm or enhancing some good in the original problem. This serves in the problem definition process.
• Function and Attribute analysis: to model the functional relationships in the system (releasing the ‘two-substance restriction’ in the Substance-Field modeling) with some inclusion of attributes of objects.

2.3 Overall Procedure of Problem Solving in TRIZ
The above description of the components of TRIZ KBs and TRIZ methods and their positions shown in Figure 2 are basically agreed in the community of TRIZ specialists [1, 7, 9, 2] . The overall procedure of problem solving in TRIZ must further specify the recommendation of ‘which methods and which KBs should be used in which order in which situation of problem.’ This is the issue on which many TRIZ leaders have proposed and applied in many different ways, and is still under a confusing situation as follows:
Altshuller [1] who developed all the individual methods and KBs in Classical TRIZ also developed the overall procedure in the name of ARIZ (Algorithm of Inventive Problem Solving). Intending to make ARIZ more and more powerful for solving ever harder problems, he constructed various versions of ARIZ having complicated procedure of using various individual methods and their corresponding KBs. He recommended to use ARIZ after at least 80 hours of training, and for solving simpler problems he advised to use more standard methods (i.e., some appropriate individual methods).

Yuri Salamatov, in his orthodox TRIZ textbook [7] , recommends to try several inddividual methods listed above and use ARIZ later only when no satisfactory solutions are obtained. Boris Zlotin and Alla Zusman [9] have proposed TRIZ Tool Map and recommended to use different individual tools depending on the type of sub-problems which are suggested by the cause-effect analysis.

Darrell Mann in his recent textbook [2] proposes a four-stage process composed of ‘define the problem’, ‘select the solution tool’, ‘solve the problem’, and ‘evaluate the solution’ stages. Though his explanation of individual methods is excellent and insightful, his overall process seems to contain two problems: Methods for problem analysis, i.e. the main part of the abstraction process in the fourbox scheme, are described separately in the ‘problem definition’ and the ‘problem solving’ stages. In the ‘tool selection’ stage, he shows 19 situations of judging the results of the ‘problem definition’ stage and recommends for each situation up to four tools to select in the ‘problem solution’ stage. The selection table is too large and complicated to summarize here.

Thus these overall procedures of problem solving in the traditional TRIZ have in common the following weak points:
• The models of solution generation in TRIZ, especially the three principal models consisted of Inventive Standards, Inventive Principles, and Trends of Evolution, are placed separately and in parallel.
• Corresponding to the separated models for solution generation, the problem analysis phase provides separate methods of analysis, and usually carries out only one for each.
• Because of separated pairs of analysis and solution generation methods, the problem is analyzed only partially for each TRIZ model. This partialness is the origin of insufficiency in the power of the TRIZ procedure, and requires a complicated sequencing of selected methods.

3. Unified Structured Inventive Thinking (USIT) as a Simple and Unified TRIZ
USIT is a simplified and unified version of TRIZ, having reorganized all the TRIZ methods for problem analysis and solution generation, having constructed a clear full procedure for problem solving, and having a clear scheme of problem solving.

3.1 Main features of USIT
USIT was developed by Ed Sickafus [8] at Ford Motor Co. in 1995 by adopting and enhancing Israeli Systematic Inventive Thinking (SIT), which was a much simplified method of TRIZ developed in early 1980s. USIT has the following features:
• USIT provides a unified and simple procedure for the whole process of problem solving in technology. The process is characterized with three phases, i.e., problem definition, problem analysis, and solution generation phases.
• In the problem definition phase, users are requested to well define a problem with statements of an unwanted effect, the target and task stated in one or two lines, a simple sketch of the problem, plausible root causes, and minimal set of relevant objects.
• The system in problem is analyzed with the basic concepts of objects, attributes, and functions. The current system is analyzed in the functional analysis for clarifying the original intention of the system design and also in the attribute analysis for revealing as much factors relevant to the unwanted effect.
• With the Particles method, i.e., a refined version of Altshuller’s SLP modeling, ideal solution is imagined first and is broken down to feasible technical solution concepts.
• Time and space characteristics of the problem are examined.
• Only five solution generation methods are used; they are Pluralization of objects, Dimensional change in attributes, Distribution of functions, Transduction, and Generalization of solution concepts.
• USIT procedure guides the group work of problem solving by stimulating people in unconventional views of the problem, for obtaining multiple conceptual solutions to real industrial problems. USIT does not depend on any handbook, knowledgebase, or software tools.

The present author [3-6] introduced USIT into Japan since 1999 and further refined it. The main features of refinement are:
• All the TRIZ solution generation methods, which are mostly represented in the principles in the TRIZ KBs, are shuffled and reorganized into the USIT solution generation methods.
• Thus USIT has a unified and simple hierarchical system of solution generation methods, expressed in the form of operators. The five principal methods for solution generation in USIT are: (1) Pluralization of objects, (2) Dimensional change in attributes, (3) Distribution of functions, (4) Combination of solution pairs, and (5) Generalization of solutions. There are 32 sub-methods in total, which are expressed in the form of operators with simple guidelines.

3.2 Problem Solving Procedure in USIT
The whole procedure in USIT is expressed in the flowchart [3] as shown in Figure 3. Problem solving in USIT is done in three distinguished phases, i.e., problem definition, problem analysis, and solution generation. In the problem analysis phase, we have three principal methods, i.e., (a) the Function and Attribute Analysis of the current system, (b) the Particles Method for considering an ideal solution first, and (c) Space and Time Characteristics Analysis. Using either (a) or (b) depending on the nature of the problem is all right, but using both (a) and (b) for any problem is highly recommended from recent practices. Sequential use of (a), (c), and (b) is the typical current practice. In the solution generation phase, the five USIT operators are applied repeatedly onto possible operands in the system or in the solution space.

The flowchart representation of USIT has been used since the initial days of USIT development. It is quite natural because the group work of problem solving in USIT is actually conducted in sessions following this flowchart. Typically, Session 1 for the problem definition phase, Sessions 2 and 3 for the problem analysis phase using the methods (a)+(c) and (b), respectively, and Sessions 4 and 5 for the solution generation phase.

3.3 Overall Structure of Problem Solving in USIT

Figure 3. Flowchart of Problem Solving Procedure in USIT

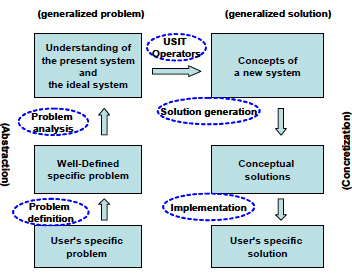
Now let us consider to map the USIT process onto the basic four-box scheme of problem solving shown in Figure 1. It is important to notice that the four boxes represent not the processes (or methods) but the information (or data) and that the arrows represent the processes. Thus we are going to draw, in terms of information science, a ‘dataflow diagram’ of problem solving in USIT: This dataflow diagram of the problem solving process in USIT demonstrates (and claims) the following points:

• Abstraction is first performed in the ‘problem definition’ phase of USIT. A user’s specific problem, which is often understood vaguely without a sharp focus by the user him/herself, is converted into a well-defined specific problem having the information stated above.
• Abstraction is further performed in the ‘problem analysis’ phase of USIT. Understanding of the present system in terms of the basic concepts of objects, attributes, functions, space and time, and also understanding of the ideal system in terms of desirable actions and properties are obtained. The information thus obtained is a generalized problem model (or an abstract problem).
• USIT has the models for problem solving in the forms of ‘USIT Operators for Solution Generation’. The guidelines of USIT Operators tell to pick up any possible operands (i.e., objects, attributes, functions, and solutions) in the system/problem and to transform them into modified operands so as to obtain pieces of concepts (or ideas) for a new system.
• Thus, in the solution generation phase of USIT, the USIT solution generation operators convert the operands in the generalized problem model into modified operands which form some parts of concepts in a new system.

• In the solution generation phase of USIT, the pieces of concepts of new system(s) are further built up into conceptual solutions on the basis of background technological capability of problem solvers. This is a part of concretization process.
• The final step of concretization is the implementation of conceptual solutions into user’s specific solution(s). This step is usually performed outside the USIT process, by filtering conceptual solutions with technological and business criteria, designing a new system, carrying out experiments, etc.

Figure 4. Dataflow Diagram to Show the Overall Structure of Problem Solving in USIT

Since the USIT Operators form the key process in this scheme of creative problem solving, the nature of them is illustrated and discussed some more detail in the following section.

4. USIT Solution Generation Operators

4.1 The hierarchical System of USIT Solution Generation Operators
The USIT Solution Generation Operators [5] form a hierarchical system as shown in Figure 5.
There are 5 principal operators which may be further classified into 32 sub-operators in total.

Figure 5. The Hierarchical System of USIT Solution Generation Operators

4.2 Illustration of Applying USIT Operators in a Simple Case: Picture Hanging-Kit Problem
Before discussing the nature of the USIT Solution Generation Operators, we better have some illustrative examples in a simple case study [6] . Let me use the Picture Hanging-Kit Problem [8] .
Our task is ‘To improve the ordinary picture hanging-kit composed of a nail, a string, and two hooks so that the picture is not apt to tilt’. Let us skip the description of the processes of problem definition and problem analysis (see Ref. [8, 3, 6] ). As the generalized problem model in this case, we have the
following pieces of information among others.
• The equilibrium position (or tilt angle) of the picture frame is determined essentially by the lengths of left and right parts of the string as divided by the nail.
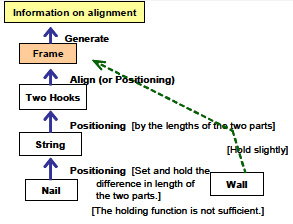
• The functional relationships in the current system may be illustrated in Figure 6.
• When the frame tilts, the string slips on the nail. If the friction between the nail and the string or between the frame and the wall is large enough, the frame may be kept at a nonequilibrium (and possibly the ‘straight-up’) position temporarily.

• Making the friction between the nail and the string large is desirable for holding the string tightly, but not desirable for adjusting the string (and hence the frame) at first.
• The nail has attributes such as length, diameter, surface smoothness, shape, material, etc. Focusing on the nail, for example, let us apply various USIT Operators. A part of such application results are demonstrated in Figure 7.
Figure 6. Functional Analysis Diagram for the Picture Hanging-Kit Problem

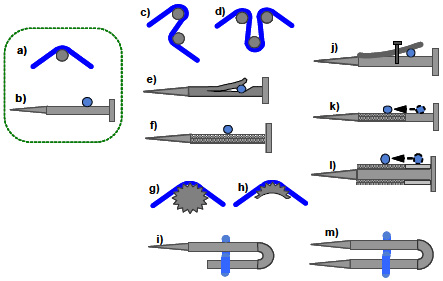
Figure 7. Illustrations of the Results of USIT Operators on the Nail in a Picture Hanging Kit

Figures a) and b) show the original nail with a string. The ‘Multiply’ operator (1b) is the simplest case of Object Pluralization (1), and gives solutions c) and d) with the intention of increasing the friction. ‘Division’ (1c) is also a form of Pluralization, and gives an idea shown in e) with the intention of holding the string tightly at the narrow slit. If we want tighter holding function after adjustment, we may attach a screw as shown in j).

The second principal operator advises ‘Dimensional Change in Attribute’, and f) is a simple response where the smoothness attribute of the nail surface is changed into a much different value, i.e. making the nail surface rough. Since rough surface is not good for adjusting, we have an idea shown in k) where only half of the nail is made rough whereas the other half is left smooth; this guides us the idea of adjusting the string at the smooth part of the nail and holding the string at the rough part. The idea l) is to use a collar having rough and smooth parts around the nail body. The surface of the nail may be changed not just rough but rugged, suggesting to change in the cross-sectional shape as shown in g). Since only the top part of the cross-section is actually used, we may change the crosssectional shape and size more drastically as shown in h). The operational idea of ‘changing shape’ of the nail gives us another solution shown in i), which effectively has two nail bodies. When I noticed that the nail i) is apt to be turned by the string tension, the idea of two-footed nail m) came up. This may be regarded as the result of ‘Unify’ operator (1d) applied on the two nails shown in c). You may notice in the above explanation that other 3 principal USIT operators have not appeared explicitly. But don’t worry. Many of the above solutions are explainable as the results of other USIT operators as well. For example, the idea k) can be explained to have been obtained in different ways as follows:
• Operator (1c): The nail is divided into two parts, and then one part is made rough while the other smooth, and they are used together.
• Operator (2d): The smoothness of the nail surface is changed to be rough and smooth at the two different parts of the nail.
• Operator (3b): The nail’s two functions, i.e., to adjust and to hold the string, are divided and assigned to two different parts of the nail.
• Operator (4b): The two opposite ideas of making the nail surface smooth for easier adjustment and of making it rough for tighter holding are combined spatially by using different parts of the nail.
• Operator (4c): The two opposite ideas of making the nail surface smooth for easier adjustment and of making it rough for tighter holding are combined temporally by pushing the string forward to the rough place after the adjustment.

In this manner, different USIT operators sometimes (or often) guide us to the same conceptual ideas. This shows the intended redundancy in the USIT solution generation operators.
For obtaining an idea, these operators may and may not be in mind explicitly beforehand. But it should be noticed that the reflection of any ideas in the general terms of these operators is important for understanding the solutions in its essence. For example, among the five ways of interpreting the idea k), the interpretation with the ‘Operator (4c): Combination in time’ is found to be most essential in this problem. This operator, in its essence, corresponds to the application of the strategy of Separation in time to a Physical Contradiction, in the orthodox TRIZ terms. Thus recognizing the idea k) in terms of this Operator of ‘Combination in time’ can lead the user to recognize the Physical Contradiction at the core of this problem and its possible elimination with the Separation in Time.
With this understanding, the user will be able to generate many more novel solutions easily.

4.3 Guidelines of the USIT Solution Generation Operators
The USIT Operators for solution generation have their guidelines (i.e., brief instruction accompanied by a schematic diagram) at the 32 sub-operator level and at even more detailed levels.
They reflect various TRIZ principles and have been reformulated in a much useful way [4, 5] . By the example, let us discuss about the ‘Divide an object’ operator (1c) in USIT. This operator has been derived from several TRIZ principles including:
• TRIZ Inventive Principle 1. Segmentation:
1A. Divide your object into independent parts.
1B. Divide your object into parts so that some its part can be easily taken away.
1C. Increase the degree of the object’s fragmentation.
• TRIZ Inventive Principle 2. Taking away
2A. Take away an interfering pat of your object.
2B. If some property of the object is undesired, find out what part of the object is a carrier of the undesired property and separate it from the object.
• TRIZ Inventive Principles 3. Local quality
3C. If two functions are to be performed by the same object but this causes problems, divide the object into two parts.
• TRIZ Inventive Principles 15. Dynamicity
15B. Divide your objects into parts capable of moving relatively each other.
• TRIZ Inventive Standards. 2.2.2 Evolution of SFM.
Increase the segmentation of the Tool substance.
• TRIZ Inventive Standards. 5.1.2 Introduction of substances under restricted conditions. Introduce a new field.
In deriving the USIT guidelines from TRIZ principles, we have chosen the following stand points:
• To use the basic USIT concepts of Objects, Attributes, and Functions in the description.
• To choose a proper level of abstraction consistently, not too abstract and not too specific.
• To describe intentions, conditions of application, applicable cases, specific examples, etc. at the level lower than the guidelines of USIT sub-operators.
Thus the guideline for the USIT Operator (1c) is described as follows:
• USIT (1) Pluralization of Objects
(1c) Divide the Object (into 1/2, 1/3, …,1/infinity):
Divide the Object into multiple parts (1/2, 1/3, …, 1/infinity), modify the parts (slightly, or differently for different parts), and combine them for using together in the system.
Some more examples of guidelines in USIT are shown for other four operators which appear in the previous subsection:

• USIT Operator (2d) Introduce a spatial attribute or vary in space:
Introduce or enhance an Attribute related to the space, or activate an Attribute (or vary the Attribute’s value) depending on different places in space (or different parts of an Object).

• USIT Operator (3b) Divide the compound Functions and assign them separately:
Divide the compound/multiple Functions present in the system and reassign the divided Functions to different Objects (already present or newly introduced) or different parts of Objects.

• USIT Operator (4b) Combine spatially:
Combine multiple solutions in respect to the spatial positions to apply; for instance, at different places (for avoiding the mutual interference), at distributed places, side by side, in front and back (in sequence), on top and bottom, at the same place alternatively, inside of the other, as an inner-structure of the other, etc.

• USIT Operator (4c) Combine temporally: Combine multiple solutions in respect to time to apply; for instance, in sequence (one after another), beforehand of the other, simultaneously (in parallel), afterwards of the other, in the reverse order, alternatively, in pulses, periodically, from time to time, interrupting/ switching corresponding to the situations, etc.

From these examples of guidelines in USIT, I hope the readers understand that a number of TRIZ principles (including Inventive Principles, Inventive Standard, Trends of Evolution, etc.) are smoothly unified in these USIT Operators, and that the solution examples shown above are easily obtainable by applying these USIT Operator guidelines.

Usefulness and intended redundancy of USIT Operators are based on the USIT concepts of Objects, Attributes, and Functions. The USIT Operators on Objects (as shown in case of (1c)) take some Objects as the operand, apply the specified operation on the Objects, and then further apply modifications onto Attributes and Functions of the operand Objects according to the guideline descriptions. Situations are similar in the USIT Operators on Attributes and on Functions. This type of extension in the USIT guideline descriptions guides the problem solver in a way easier to follow than most TRIZ principles. At the same time, the mentioning of Objects, Attributes, and Functions in each guideline description is the source of intended redundancy, i.e. overlapping, of the USIT Operators.

4.4 Experiences of Teaching and Applying USIT
Experiences of teaching and applying USIT in Japan have been reported in [3, 6] . A lecture of 2 hours can cover the overview of TRIZ and USIT. Typically, two-day USIT training seminar is held in a company with 15-25 participants of engineers. After the overview lecture, 3 real industrial problems are brought in by the participants and are tried to solve in parallel group practice following the USIT procedure. 5 sessions are carried out, where each session is composed of a short lecture of the process, parallel group practice, and presentation & discussion. Usually each group generates 20 to 40 ideas which may be further concentrated into several conceptual solutions worthy of further consideration for implementation. Thus engineers, who were novice of TRIZ/USIT, can have the experience of solving an industrial problem with USIT by themselves, and can understand the full USIT procedure with 3 real case studies. This shows the easiness and effectiveness of learning USIT in comparison with learning TRIZ.

5. Concluding Remarks
In the basic four-box scheme of problem solving, generalized models of TRIZ (and many other scientific/technological theories) are expressed by the generalized problems and their corresponding generalized solutions, and are supposed to be used with analogical thinking. Abstraction is for mapping the user’s specific problem to the generalized one in the model, while concretization is for mapping backwards. These mapping processes, however, are often not well explained in the procedural manner.
The present paper proposes a different scheme of problem solving, as summarized in Figure

Figure 8. Scheme of Problem Solving in USIT Using the USIT Solution Generation Operators Abstraction is done in two steps; the problem definition step converts the user’s specific but often vague problem into a well defined specific problem and the problem analysis step converts it further into the abstract understanding of the current and ideal systems. This abstract understanding of the system is expressed in the basic terms of objects, attributes, functions, space, time, desirable actions, and desirable properties, etc. and is in place of the generalized problem of the four-box scheme. Then the Solution Generation Operators in USIT transform the elements of the abstract system into modified elements of a new solution system; this is the key step in the whole problem solving. Then conceptual solutions are formed on the basis of technological thinking, and finally user’s specific solutions may be designed in technology.

It should be noticed that the vagueness in the analogical thinking disappear in the new scheme. Knowledge expressed in the ‘Models’ in TRIZ (and problem solving methods in general) has been concentrated into the USIT Operators. And hence all the procedures of creative problem solving are now expressed in much clearer terms and procedures.
This unification and simplification of TRIZ can help people understand TRIZ more easily and
widely and apply TRIZ to their real problems, as demonstrated earlier.

References
[1] Genrich Altshuller: “Creativity as an Exact Science”, Gordon &Breach, 1984 (E).
[2] Darrell Mann: “Hands-On Systematic Innovation”, CREAX Press, Ieper, Belgium, 2002 (E); Japanese edition, SKI, Tokyo, 2004 (J).
[3] Toru Nakagawa: ‘Experiences of Teaching and Applying the Essence of TRIZ with Easier USIT Procedure’, TRIZCON2002: Fourth Annual Altshuller Institute for TRIZ Studies International Conference, Apr. 30- May 2, 2002, St.Louis, MO, USA; TRIZ HP Japan, May 2002 (E); Jan. 2002 (J).
[4] Toru Nakagawa, Hideaki Kosha, and Yuji Mihara: ‘Reorganizing TRIZ Solution Generation Methods into Simple Five in USIT’, ETRIA World Conference “TRIZ Future 2002” held at Strasbourg, France, on Nov. 6- 8, 2002; TRIZ HP Japan Nov. 2002 (E); Sept. 2002 (J).
[5] Toru Nakagawa, Hideaki Kosha, and Yuji Mihara: ‘USIT Solution Generation Methods: Simplified System by the Reorganization of TRIZ Solution Generation Methods’, Appendix to Ref. [4] , ETRIA World Conference “TRIZ Future 2002” held at Strasbourg, France, on Nov. 6-8, 2002; TRIZ HP Japan Nov. 2002
(E); Sept. 2002 (J).
[6] Toru Nakagawa, Hideaki Kosha, and Yuji Mihara: ‘Usage of USIT Solution Generation Methods: A Simple and Unified System of TRIZ’, TRIZCON2003, held at Philadelphia, USA, on Mar. 16-18, 2003; TRIZ HP Japan, Apr. 2003(E); Jan. 2003 (J).
[7] Yuri Salamatov: “TRIZ: The Right Solution at The Right Time”, Insytec, The Netherland, (1999) (E); Japanese translation, Nikkei BP, (2000) (J).
[8] Ed. N. Sickafus: “Unified Structured Inventive Thinking: How to Invent”, NTELLECK, Grosse Ile, MI, USA, (1997).
[9] Boris Zlotin and Alla Zusman: “Tools of Classical TRIZ”, Ideation International Inc., Southfield, MI, USA, (1999) (E); Japanese translation, Nikkei BP (2000) (J).