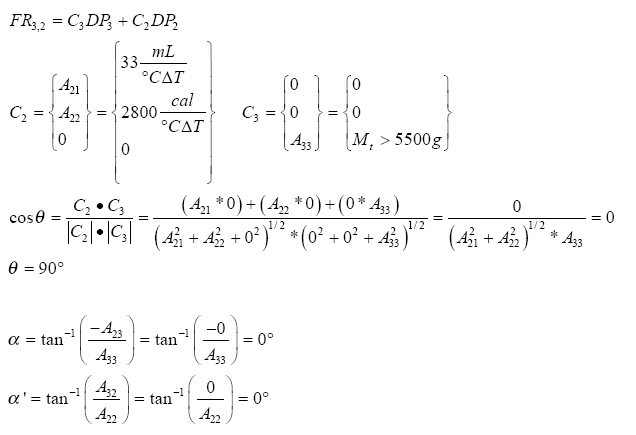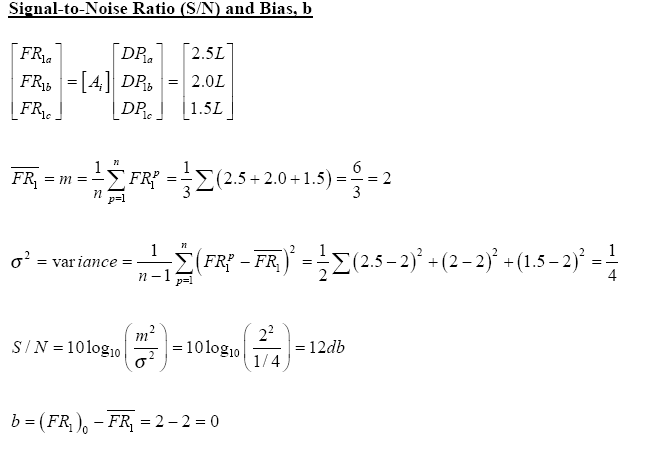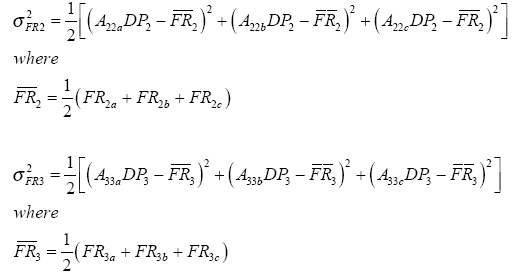Editor | On 02, Jun 2003

By: Michael Slocum, Catherine Lundberg, Katrina Walter

Abstract:
The calculation and use of Ideality to drive the evolution of a technological system can be a subjective process. The identification and definition as an element as useful or harmful can be convoluted and non-repeatable when calculated by different members of the design team. Also, there is not standardization of this technique that would yield consistency across product domains. Axiomatic Design was employed to create a robust disposable self-heating chafing dish for use by consumers. This paper compares the standard combustible fuel disposable chafing system with a self-heating disposable chafing system in order to demonstrate the key elements of the Axiomatic Design Process. This demonstration evolves into the use of Reangularity and Semangularity (metrics of the degree of coupling in a system between design elements) to apply a rigorous standard to the calculation and effectiveness of Ideality. The results of this effort are considered to be the primary intent of this paper.

A Brief Review of Axiomatic Design and its’ Application to Ideality
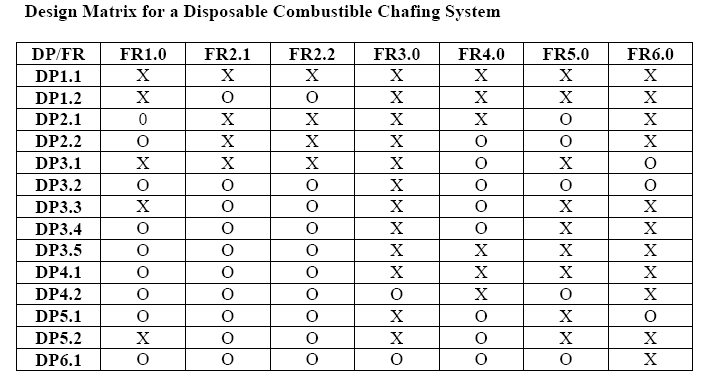
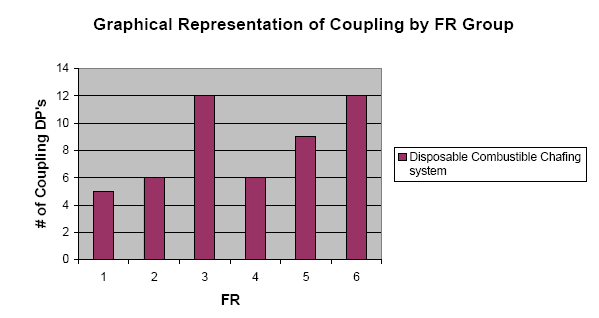
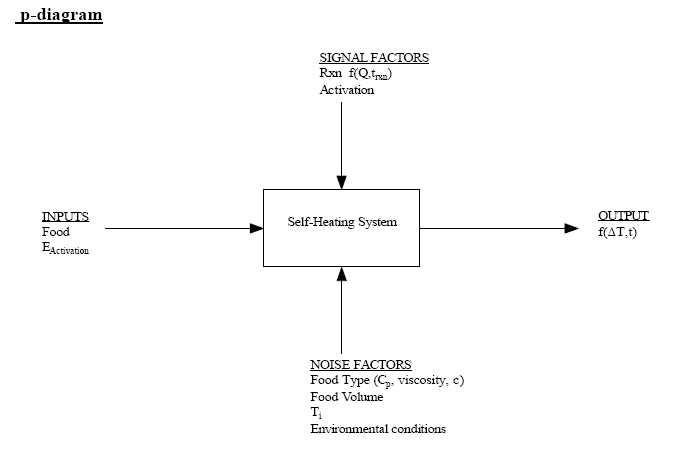
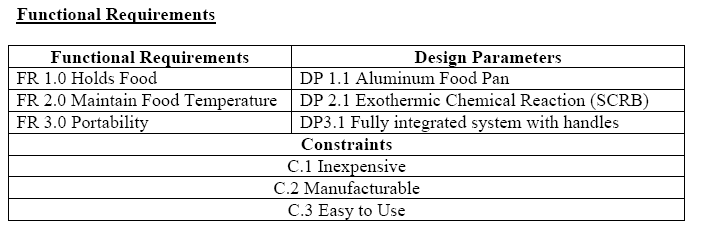
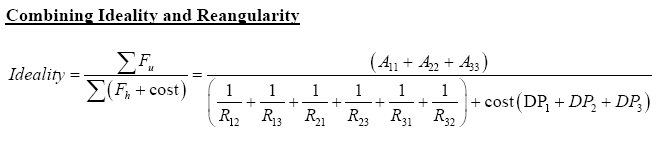
Axiomatic Design is a system that uses design axioms and corollaries to govern the design process. The two main axioms govern dependencies between functional requirements (FR’s) and design parameters (DP’s) and the total information content of a system. The FR-DP dependencies should be maintained on a one-to-one basis with no cross-correlation between FR’s and DP’s (independence). When cross-correlations occur this is called “coupling”. The degree of coupling is an indication of the state of the design with the desire that coupling either not exist or exist at a very minimal level. The structure and mapping of the elements in Axiomatic Design is well established, therefore, it is possible to consistently apply this technique to a system. This consistency lends itself to application in the Ideality element of TRIZ. The useful functions of a system would be categorized with the inclusion of a DP for each element thereby supplying the information of the numerator of the Ideality equation. Those elements that are indicative of coupling would be included in the denominator with the costs associated with each DP:

TRIZ offers algorithms for the creative resolution of problems, the evolution of a technological system, and the ideal final result concept but there is no rigorous application of axioms to the correspondence of requirements and parameters. This core feature of Axiomatic Design when incorporated with the creative elements of TRIZ will enable the practitioner to increase the idealness of the their system.

Axiomatic Design Axioms
1. The Independence Axiom – Maintain the independence of FRs
2. The Information Axiom – Minimize the information content of the design

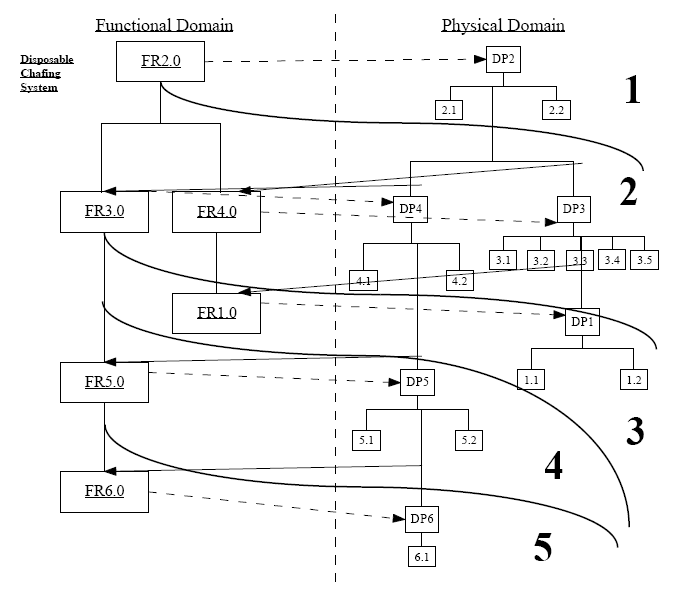
· This flowchart outlines the design progress
· The DP’s from the previous FR feeds into the next FR’s
· Analyze the design at each of the 5 levels.

Information Content (Partial)
The partial information content was calculated utilizing the above described equation and data from Buffet Test #1 and #2. The rating was considered acceptable if the food was rated between 2 and 4 (rating scale was 1-5, cold to hot).

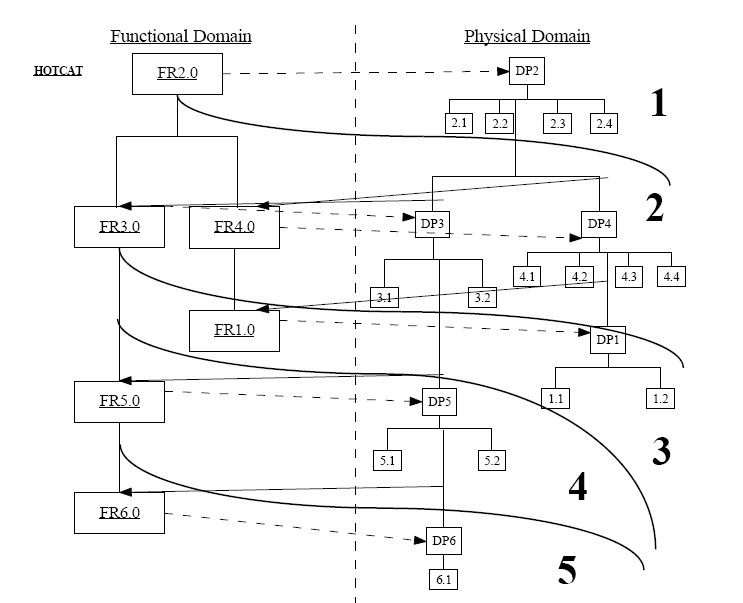
Removing FR’s 3.0, 5.0, and 6.0
FR’s 3.0, 5.0, and 6.0 could be considered system constraints instead of FR’s. The above
analysis is repeated after the removal of these FR’s. The new FR’s are as follows:

Disposable Combustible Fuel Chafing System

Our design has FR

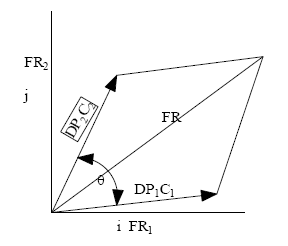
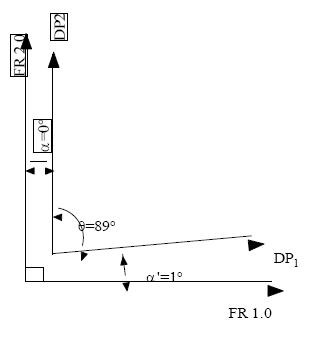
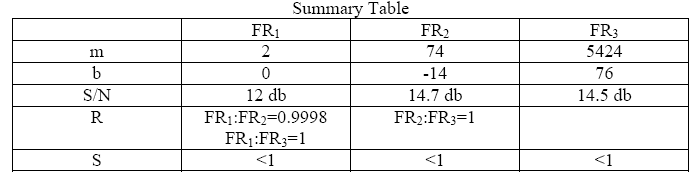
Reangularity, R is a value that has an inverse relationship to coupling (i.e. as reangularity decreases, coupling increases). If R is 0, the design is completely coupled. If R and S are unity, 1 then the design is uncoupled. Reangularity is defined by the following:

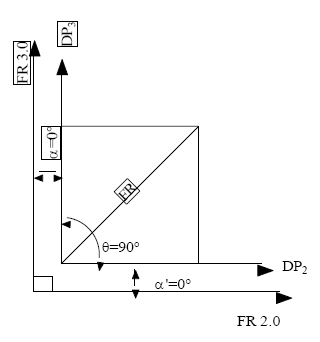
This information combined with the design equation 1.0 and corresponding matrix to create isotherms utilizing the following the methodology outlined in the following 2- dimensional example: