Editor | On 15, May 2006

Toru Nakagawa
Osaka Gakuin University, Japan

First Presented at The 27th Annual Conference of the Japan Creativity Society held on October 29-30, 2005 at National Center of Sciences, Tokyo (in Japanese); Posted in the TRIZ Home Page in Japan on November 30, 2005 (in Japanese). Translated into English by Toru Nakagawa on April 23, 2006;
Posted in the TRIZ Home Page in Japan on April 25, 2006 (in English).

Abstract
As a basic scheme for Problem Solving, the ‘Four-Box Scheme’ which advises to generalize the problem first into an abstract level and then to concretize it back has been widely accepted. The contents of the Four Boxes in this scheme, however, have not been well established in existing problem solving methodologies, which include analogical thinking utilizing with knowledge bases, Ichikawa’s Equivalent Transformational Theory trying to extract essence from hints, and TRIZ (Theory of Inventive Problem Solving). TRIZ is typically faced with a confusing situation in its overall process due to having a large variety of techniques.
After the reflection of this situation, the overall structure of USIT (Unified Structured Inventive Thinking) has been represented in a dataflow diagram, and modeled to obtain the ‘Six-Box Scheme of Creative Problem Solving in USIT’. The scheme clearly describes the information requested/generated in the six boxes along the full process of problem solving; they are the processes of defining the problem in the real world, analyzing the problem in a standardized manner, generating elements of ideas by applying USIT Operators, building conceptual solutions around the core ideas, and finally implement the solutions in the real world. The new scheme, being a much refinement of the basic ‘Four-Box Scheme’, provides a ‘New Paradigm for Creative Problem Solving’.

1. Introduction
In the fields of science and technology, the ‘Four-Box Scheme of Problem Solving’ has been accepted as an authentic model, where the problems are to be solved in an abstract level as shown in Fig. 1. The Specific Problem in the real world is firstly abstracted into a ‘Generalized Problem’, and is solved to get a ‘Generalized Solution,’ and is finally concretized

Fig. 1. Basic Four-Box Scheme of Problem Solving

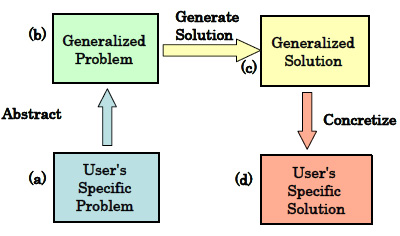
back into a real Specific Solution to the original problem.
The present paper has examined the contents of the basic Four-Box Scheme, and is advocating a new paradigm, named as ‘Six-Box Scheme of Creative Problem Solving (in USIT)’ in technological fields. The new scheme defines the contents of the boxes more clearly and provides concrete ways of processing the information between the adjacent boxes.
Before reaching the new scheme, the present author examined the schemes of (a) analogical thinking with use of knowledge bases, (b) Equivalent Transformational Thinking developed by Kikuya Ichikawa [1, 1a] , (c) TRIZ by Genrich S. Altshuller [2, 2a] , and USIT by Ed Sickafus [3, 3a] . The present proposal is based on our refinement of USIT [4] and has been obtained through our new understanding of the basic scheme for creative problem solving [5] .
We should note here the importance of using two different types of representation of basic scheme of problem solving methodologies. On one hand we use the representation of processes (e.g., in the flowcharts), while on the other hand we use the representation of information to be dealt or generated in the processes (e.g., in the dataflow diagram, such as shown in Fig. 1).

2. Knowledge Base Utilization and Analogical Thinking
First, let us examine the underlying ways of applying various existing methodologies and clarify the real situations of usage of the basic Four-Box Scheme.
Generalized Problems and their corresponding Generalized Solutions used in the scheme are called with various names, such as theories, models, templates, examples, etc., and have been built and accumulated in every field of disciplines. As the extension of disciplines into more and more segmented details and as the accumulation of huge knowledge bases, the basic scheme of problem solving has practically shifted towards the one shown in Fig. 2.

Fig. 2. Four-Box Scheme of Problem Solving Using Models in the Knowledge Bases

In short, the knowledge base contains a large number of pairs of ‘Generalized Problem and its Generalized Solution’ (i.e., Models) and hence finding an appropriate pair is required in using the scheme of Fig. 2.
In cases of limited types of problems in theoretically well established fields of mathematics and physics, the problem may be abstracted in an established way in the discipline, passed through a well-known pair of ‘Generalized Problem and its Solution’, and transferred into some specific problems in most cases.
However, as being discussed in the present paper, for many problems which require creative problem solving, it is not obvious which models are appropriate to use. And different models often request different ways of abstraction. After having tried several conventional models without success, we encounter a real inventive problem.
Then we have to select some model, either intuitively or with trial-and-error, and to analyze (i.e., to abstract) the problem in a manner required by the model. Selection of the model is often related to searching for a hint or to encounter an enlightenment on some unexpected occasion.
When we search for a model in this manner and try to use a model, we typically apply the Analogical Thinking. We first find (or select) a model as a hint, then try to extract some common nature in the model and in our specific problem, and to adopt good points of the hint to build our solution to the problem.
The Analogical Thinking has neither reliable guideline for finding appropriate hints nor clear ways for the abstraction and concretization processes; thus it stays at the naive stage of intuition and feeling.

3. Ichikawa’s Equivalent Transformational Thinking; A Brief Review
Kikuya Ichikawa (1915-2000, Japan) tried to overcome the weakness of Analogical Thinking and to establish a new scheme for creative problem solving. He named his scheme ‘Equivalent Transformational (ET) Thinking’ [1, 1a] .
He represented his scheme in a form of mathematical equation (ET equation), as shown in Fig. 3, accompanied with explanation of symbols.

Fig. 3. Equivalent Transformational Thinking Developed by Kikuya Ichikawa

The present author, being a researcher outside of his group, has represented the ET equation in a diagram easier to understand in the common sense, as shown in Fig. 4. This ET diagram principally describes the Information to be used; thus it is a kind of ‘dataflow diagram’ (instead of a flowchart, or a ‘process-flow diagram’). The method of processing is shown with the arrows and numberings, in reference with Ichikawa’s ET flowchart.

Fig. 4 Overall Structure of Ichikawa’s Equivalent Transformational Thinking (Drawn by Nakagawa)
According to the ET Thinking, we first set up a view (Vi) of the problem to solve, clarify the target function (ε), and then go ahead to search (in different fields) for a concrete case having the function. The concrete case A is now used as a hint. Specific details of the case A are now thrown aside, while essential conditions (c) (i.e., principal means of performing the function) and the target function (ε) are extracted. The essence ‘cε’ should be expressed
in the verbal form of ‘Action – Object – Means’ and may be regarded as (the core part of) the Generalized Solution in the Four-Box Scheme in Fig. 1. Using this as the core of solution, we further introduce technical knowledge in order to construct a Specific Solution B applicable to our Specific Problem.
As briefly explained above, the ET Thinking has provided a conceptual guideline to abstract a Specific Case A for clarifying its functional essence ‘cε’ and to concretize the idea into a Specific Solution. However, since it searches for a specific case as a hint and tries to construct a solution depending on the hint, the ET Thinking still largely keeps the framework of the Analogical Thinking.

4. Review of Basic Schemes of TRIZ and USIT
TRIZ is a Methodology for Creative Problem Solving, developed in ex-USSR by Genrich S. Altshuller and his followers. They have built ‘TRIZ Knowledge Bases’ of science and technology by reorganizing the knowledge in various useful frameworks and have developed a variety of techniques for creative problem solving [2] . The basic scheme of problem solving in TRIZ is represented in Fig. 2.
TRIZ has several sets of rich and useful knowledge bases, such as Inventive Principles, Inventive Standards, and Trends of Technological Evolution; each set of knowledge base also has its own appropriate method of preprocessing for problem analysis/abstraction. The contents of these knowledge bases and the methods for using them are understood well in the community of TRIZ experts.
However, the overall process (i.e., the flowchart representation) of problem solving in TRIZ is in a confusing situation. Ways of sequentially performing several pairs of ‘knowledge base and its pre-analysis method’ are very complex, and different ways of performing the ‘knowledge base and analysis method’ pairs according to the classification of problem cases are no simpler. Even though such ways are powerful for TRIZ experts, they are too complex to understand and to apply for ordinary engineers.
When one tries to represent the overall structure of problem solving in TRIZ in a Dataflow diagram, parallel and alternative components expanded from several sets of knowledge bases and their analysis methods make diagram too complex. The present author pointed out that this is the root cause of difficulty in the TRIZ methodology [5] .
There have been trials to simplify and reorganize TRIZ into a simpler and yet effective methodology for problem solving. USIT (Unified Structured Inventive Thinking) is such a methodology, originally developed by Ed Sickafus at Ford Motor Co. [3, 3a] . The present author has been working for improving USIT further [4, 5] .
Sickafus built the overall process of USIT problem solving procedure in clear three stages, i.e., Problem Definition, Problem Analysis, and Solution Generation stages, and introduced concise methods in each stage. He quitted using TRIZ knowledge bases as the principal means of problem solving, and built up guidelines of thinking procedures for engineers; thus
he tried to build a new methodology for creative problem solving.
For the Problem Analysis stage, the concept of Objects-Attributes-Functions has been used for underlying the methods of Functional Analysis and Attributes Analysis of the present system. Characteristic nature (or uniqueness) in Space and in Time is analyzed. And a technique (the Particles Method) is introduced to make an image of ideal solution first and to think how to realize it with the help of a thinking tool of ‘Magical Particles’ (i.e., an improvement of Altshuller’s Modeling with Smart Little People).
At the Solution Generation stage, USIT uses simple five methods, which were refined from the preceding Israeli SIT method.
Contributions of the present author to the improvement of USIT are most relevant to the Solution Generation methods [4] . We have examined all the elements of solution generation methods in the rich knowledge bases of TRIZ and classified them individually into the framework of USIT solution generation methods. Then the rich contents of the USIT five methods have been classified further to construct a hierarchical system of solution generation methods. Thus USIT has a system of 5 methods containing 32 sub-methods in total. Each sub-method has a simple guideline how to apply it. (For example, one of the sub-methods in the Object Pluralization Method is described in its guideline as ‘Divide the object into multiple parts, then change them differently in their attributes, and finally use them in an integrated way’.) These solution generation methods in USIT are called the ‘USIT Operators’.
Since the early stage of USIT development, the whole USIT procedure has been represented in the flowchart for active use in practice .
For a long time, however, neither Sickafus nor the present author have had the concept of ‘Basic scheme of problem solving in USIT’. As mentioned above, the present author realized that TRIZ does not have a concise overall structure and hence TRIZ faces with a serious confusion in its overall procedure. Then the present author has drawn the overall structure of USIT in a dataflow diagram and found it structured clearly.
The present author has realized various implications of the Overall Structure of USIT represented in the dataflow diagram. The diagram has guided us to the understanding of ‘A New Basic Scheme (or Paradigm) of Creative Problem Solving’. The concept is the topic of the present paper and is described in the following.

5. Overall Structure of Problem Solving in USIT
The Overall Process of USIT is represented in the form of flowchart, as shown in Fig. 5.

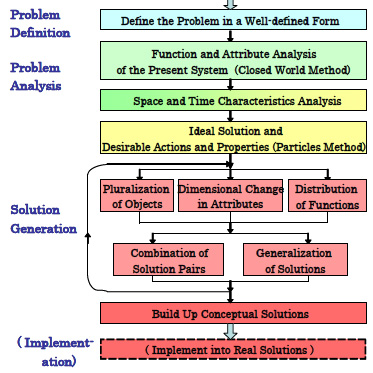
Fig. 5. Overall Process of Problem Solving in USIT (Flowchart Representation)

Each box in Fig. 5 represents a process which can be performed with some supporting technique. At the Solution Generation stage, USIT has 5 principal methods (shown in two groups); by applying them repeatedly without any fixed order, (pieces of) ideas of solutions are generated one after another. Then by virtue of technical backgrounds the ideas are converted into Conceptual Solutions, or solutions at a conceptual level.
For describing the information required or generated in each process, the Overall Structure of USIT is now represented in the form of dataflow diagram, as shown in Fig. 6.

Fig. 6. Overall Structure of Problem Solving in USIT (Dataflow Representation)

= Six-Box Scheme of Creative Problem Solving in USIT = New Four-Box Scheme of Creative Problem Solving
In this figure, the boxes describe the Information while the arrows and accompanied ovals represent the Processes. (Note that the broken-line enclosures are explained later in Section 6(2).) The contents of the boxes are explained as follows:
(a) The first box represents ‘User’s Specific Problem’: The user recognizes some problem in the real world and decides to solve it. The information gathered by the user at this initial stage is often detailed and complex and not organized well.
(b) ‘User’s Well-defined Specific Problem’ in the second box represents the information of the problem which is set up and focused to be solved in USIT. USIT requests the user to clarify the following points of information in the problem: an unwanted effect (causing the problem/difficulty); a target statement of the problem to be solved; a simple sketch of the problem system for clarifying the mechanism of the problem; plausible root causes; a minimal set of objects (or system components) containing the problem.
(c) The third box represents the information resulted through the analysis of the problem. First, Function Analysis of the present system (i.e., the system having the problem, or a system expected in the present technology) provides the information about the functional relationships among the objects and about the overall mechanism of the system (and its defects). Attribute Analysis clarifies the attributes which may increase or decrease the problem’s unwanted effect. Examination of the problem in terms of Space and Time derives the information of characteristic (or unique) nature of the system. Furthermore we analyze an image of ideal solution and obtain the information of solution directions. Even though we do not know yet the means to achieve the ideal solution at this stage, we obtain the information of desirable actions (or behaviors) and desirable properties of the ideal solution.
(d) In the fourth box, we have ‘Ideas for a New System’, which mean the information of pieces of ideas for a possible solution system at the preliminary stage without examining their implementation methods and their feasibility yet. Such ideas do not stand alone but instead come out as the ‘seeds of new changes’ with the background of all the information shown in the previous boxes. In the USIT procedure, multiple of these ideas are generated by applying various USIT Operators repeatedly.
(e) ‘Conceptual Solutions’ in the fifth box represent new solution concepts constructed around the core ideas mentioned in the previous box. For constructing such solutions, a certain level of technical capability in the relevant fields is of course necessary. The solutions at this stage are still qualitative and conceptual; quantitative examination and details of design need to be made at the later stage.
(f) ‘User’s Specific Solutions’ represent the solutions at the level of being implemented in the real world. They are the solutions to the problem in the real world, such as new improved products or their components, new devices or processes for production, etc. However, the solutions at this stage are outside of the range of USIT as a methodology for Creative Problem Solving. This means that the final results of USIT are the solutions shown in the previous stage (e).
The Overall Structure of USIT is represented in Fig. 6 in the form of dataflow diagram; this scheme is named the ‘Six-Box Scheme of Problem Solving in USIT’. Its advantage is the fact that the contents of Information in each box of the scheme are specified much more clearly than in the Four-Box Scheme shown in Fig. 1. Furthermore, the procedural methods for obtaining these items of information step by step are already established in USIT [3, 3a, 4, 5] .

6. Implications of the ‘USIT Six-Box Scheme’
Figure 6 showing the Overall Structure of Problem Solving in USIT has been found to have a variety of implications. Understanding of such implications are explained in the followings:
(1) The first major point of understanding is the recognition that the diagrams describing the information for inputs and outputs (e.g., dataflow diagrams) are, in general, more important and fundamental than the diagrams representing the processes (e.g., flowcharts).
The description of the input/output information specifies the constraints and targets of the process. As far as the process satisfies the input/output specifications, it may be implemented in different ways. Thus, various processing methods may be tried in each step of procedure; this means that the flowcharts are revised but the dataflow diagram stays the same. Hence it is most important to specify the major stages of problem solving and their required information; such specification is called the ‘Overall Structure’ or ‘Basic Scheme’ in the present paper.
(2) The second implication becomes clear when we enclose, as shown in Fig. 6, the two boxes at the bottom-left and the two boxes at the bottom-right, respectively. This derives a ‘New Four-Box Scheme’. The bottom-left box enclosed with a broken line shows that the ‘User’s Specific Problem’ is still vague and need to be defined more clearly into the ‘Well-defined Specific Problem’ at the starting point of Problem Solving in USIT. Similarly, the bottom-right broken-line box shows that the ‘Conceptual Solutions’ obtained as the direct results of Creative Problem Solving are still at a conceptual level and need to be improved further in the Implementation stage into usable Real Specific Solutions.
Using the broken-line boxes, the scheme shown in Fig. 6 corresponds well with the Basic Four-Box Scheme shown in Fig. 1. In our New Four-Box Scheme in Fig. 6, the information represented with the boxes and the processes shown with the arrows are specified in clearly defined terms, in contrast to the fact that those in Fig. 1 are described only in general abstract terms. This means that Figure 6 has described clearly for the first time a ‘Basic Scheme of Creative Problem Solving’.
(3) The third implication is related to the understanding of the ‘Generalized Problem’ in Fig. 1. Figure 6 claims that such information of Generalized Problem is obtained from User’s Specific Problem as the result of a standard process of Problem Analysis. The Problem Analysis methods in USIT are common and standardized, and thus learnable in USIT textbooks, while the contents of the ‘Generalized Problem’ come solely from User’s Specific Problem. Such contents do not come from the models in knowledge bases or textbooks as suggested in Fig. 2, and they are not extracted from a different case used as a hint as suggested in Fig. 4.
(4) The fourth implication is related to the nature of the ‘Generalized Solution’ in Fig. 1. In our new scheme shown in Fig. 6, the top-right box is not a well-structured reference-model solution but rather a piece of new idea, or an essence of enlightenment, with the background information shown in the top-left box. It should be noted that the ‘Generalized Solution in the Model’ in Fig. 2 may be regarded in the ET Thinking as the ‘Specific Case Ao to be used as a hint’. And the ‘Essential Condition and Target Function cε’ extracted from the hint in ET corresponds to the ‘Ideas for a new system’ in USIT, as shown in Fig. 6. In USIT, we understand that such ideas are born to birth directly by applying the ‘USIT Operators’.
The transformation of the Ideas into Conceptual Solutions is described in the ET Thinking as the ‘Reconstruction’ which is facilitated with the knowledge of Specific Conditions in the target system B. Our scheme shown in Fig. 6 is close to the understanding in the ET Thinking. However, much of the information necessary for the transformation from Ideas to Conceptual Solutions have already been prepared in USIT as the results of the Problem Analysis, i.e., the top-left box in Fig. 6.
(5) The fifth implication is illustrated in Fig. 7.

Fig. 7. Roles of the Real World and the Thinking World in the Creative Problem Solving

The lower 4 boxes belong to the ‘Real World’ where are involved society, businesses, and technologies among others. Thus which problem among many we should tackle with should be decided and focused against the criteria of the Real World instead of the Thinking World of USIT. When a problem is brought in to the problem solving session, however, the target and focus of the problem is very often still vague and not examined well. For this reason the USIT procedure has the stage of Problem Definition at first in order to make the focus of the problem clear and to make the target of the problem a consensus in the problem solving team. It should also be remarked that after the creative problem solving procedure in the Thinking World, the Conceptual Solutions thus obtained must be examined and improved before implementation in the Real World with the criteria of technologies, businesses, and society, etc.
The upper four boxes in Fig. 7 belong to the ‘Thinking Word’ for Creative Problem Solving (in USIT). One should better set various Real-World constraints aside for a while during the Creative Problem Solving activities in order to think as flexibly and creatively as possible. The two boxes in the middle of Fig. 7 serve as the interfaces of information between the two Worlds.
(6) The sixth implication is demonstrated in Fig. 8. The three boxes on the left side represent the processes of Abstraction (or Analysis) of the User’s Specific Problem which result in the generation of deeper understanding of the present and ideal systems (in terms of Objects, Attributes, Functions, Space, Time, etc.). These processes should be led primarily by the problem solving method, but require correct understanding of mechanisms and technologies of the problem. On the other hand, the three boxes on the right side represent the process of Concretization (or Synthesis) starting from some elements of core Ideas, generating Conceptual Solutions, and finally implementing into Real Specific Solutions. During these processes, the creative problem solving methodology has a relatively minor role in comparison to the major role of knowledge and facilities in the

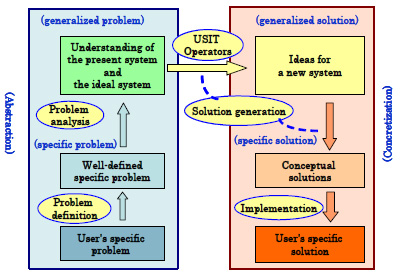
Fig. 8. Abstraction, Idea Generation, and Concretization for the Creative Problem Solving

relevant technologies.
The transfer (or jump) from the understanding of the present system to Ideas for new systems is assisted by the USIT Operators. While the USIT Operators as a whole have a well-structured hierarchical system, a piece of idea at the core of a new system can be generated by applying a USIT Operator. Individual USIT Operators are very simple, such as the operation of dividing an object, of combining a solution pair with respect to time, etc. It is well known that even great inventions in history were often generated starting with simple and small ideas in their essential cores. Applying USIT Operators inspires the engineers to generate pieces of core ideas for new systems one after another. Inspiring such number of jumps easily after a thorough analysis of the problem is the essence of the present ‘Six-Box Scheme of Creative Problem Solving’.

7. Conclusion: New Paradigm for Creative Problem Solving
The Six-Box Scheme, illustrated in Fig. 6 and explained about its implications in Sections 5 and 6, represents a ‘Basic Scheme for Creative Problem Solving’. The present paper proposes it as a ‘New Paradigm for Creative Problem Solving’. A practical procedure performing the Scheme has already been established as USIT.

References
[1] Kikuya Ichikawa: “Science in Creativity: Illustrated Introduction to Equivalent Transformational Thinking”, NHK Publishing, Tokyo, 1970 (J).
[1a] Kikuya Ichikawa: ‘Methodology of Creative Thinking: Theory of Equivalent Transformational Thinking’, Energy, Vol. 3, No. 4, Esso Standard Oil, 1966 (J); TRIZ HP Japan, Sept. 2001 (J).
[2] Genrich Altshuller: “Creativity as an Exact Science”, Gordon & Breach, 1984 (E).
[2a] Darrell Mann: “Hands-On Systematic Innovation”, CREAX Press, Ieper, Belgium, 2002 (E); Japanese edition, translated by Toru Nakagawa et al., SKI, Tokyo, 2004 (J).
[3] Ed Sickafus: “Unified Structured Inventive Thinking: How to Invent”, NTELLECK, Grosse Ile, MI, USA (1997).
[3a] Ed Sickafus: “Unified Structured Inventive Thinking — An Overview”, eBook, URL: http://www.u-sit.net/, (2003) (E); translated into Japanese by Keishi Kawamo, Shigeomi Koshimizu, and Toru Nakagawa, TRIZ HP Japan, Oct. 18, 2004 (J).
[4] Toru Nakagawa, Hideaki Kosha, and Yuji Mihara: ‘Reorganizing TRIZ Solution Generation Methods into Simple Five in USIT’, ETRIA World Conference “TRIZ Future 2002” held at Strasbourg, France, on Nov. 6-8, 2002 (E); TRIZ HP Japan, Sept. 2002 (J), Nov. 2002 (E).
[5] Toru Nakagawa: ‘Overall Dataflow Structure for Creative Problem Solving in TRIZ/USIT’, TRIZCON2005, Altshuller Institute TRIZ Conference, Detroit, May, 2005 (E); TRIZ Journal, May, 2005 (E); TRIZ HP Japan, May, 2005 (J).
Note: “TRIZ HP Japan” represents: “TRIZ Home Page in Japan”, Editor: Toru Nakagawa. http://www. osaka-gu.ac.jp/php/nakagawa/TRIZ/eTRIZ/ (in English), http://www.osaka-gu.ac.jp/php/nakagawa/TRIZ/ (in Japanese).
Note: (E): written in English, and (J): written in Japanese.