Editor | On 30, Dec 2005

By: Simon Dewulf

Introduction
The ‘Variation’ part of Directed Variation® is closely linked to Attribute Listing (early 1930’s), the technique in which a product or a system is divided into parts, and alternatives ways of achieving each (sub) function are evaluated, recombining to new variants of the product or systems.

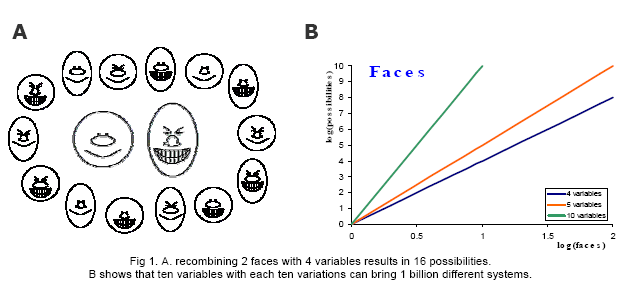
Selection becomes an issue even with few variables and limited variations, the possibilities grow exponentially. Simply put, consider 4 variables with binary variations, this will result in 16 systems (incl. the initial systems). Fig. 1 A below exemplifies two faces (binary variation) of 4 variables (nose, eyes, month and head shape) given no subtractions or additions can be made. A variety of 16 different faces can be created. Fig 1 B illustrates the exponential relation between variables and variations; 10 variables with each 10 variations produce one billion possibilities.

Whilst eliminating some attributes or properties with lesser importance, the problem of selection is a addressed with the extension of the technique; Morphological Analysis;. However, the technique gives limited difference and easily falls back into arbitrarily choosing permutations.

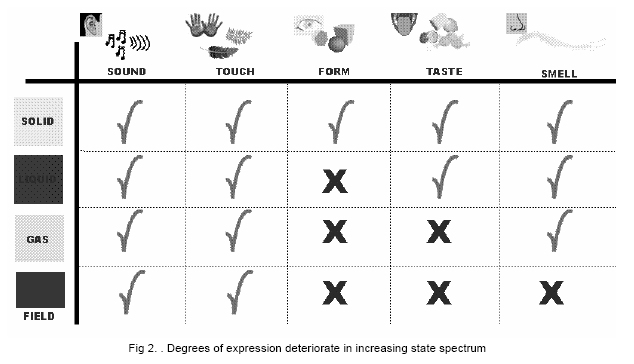
Value engineering has brought hierarchy in the functions wanted. Similarly, in Directed Variation functions are related to properties. Therefore one can greatly reduces the options or at least prioritise the variations. If your main function describes degrees of expression like shape, smell, taste or touch, variations in the state spectrum will be deteriorate the more they evolve towards field (see Fig 2). Though if energy efficiency is the main function, then the variations will improve towards field.

Selection by elimination or function
Directed variation translates the variables into property spectra, in which every property is linked to one or more functions. Let us assume we can identify 10 properties of a system (example property ‘porosity’), which each can vary in a scale of 3 (example full hollow porous). The amount of different combinations can be calculated by number of properties to the power of variations, i.e. 3^10 = 59049. As a case example, (and not toothbrush for once) let us consider a bicycle frame.

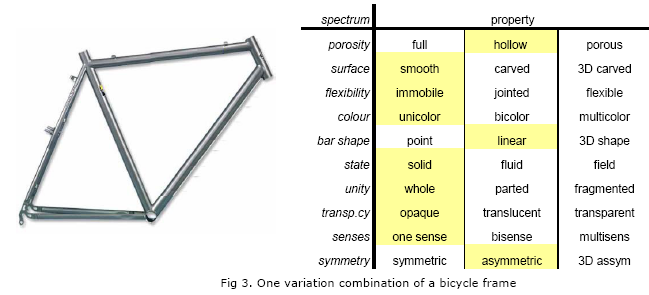
Again, although the table in figure 3 appears rather simple, 59049 variations can be made. (3^10) But just like chess, only some moves are winning. One way to start is to look at the possible variations and run a patent search. Flexible frames, jointed, segmented, curved or carved frames will surface. (Figure 4). This search is limited and mostly describes only one property in which a variation has a claimable function. The main function is strength, holding the bicycle together, then the variations expressed in liquid frame and field frame, lose the shape stability, can be eliminated, dropping 39366 possibilities. As possibilities grow exponentially, selection by elimination reduces the options exponentially. One variable has dropped 59049 options to 19683. (3^9)

Selection by patent search
As discussed in the DIVA October 2005, Directed Variation® has extracted all methodological jargon, which allows to browse data sources in a much easier way. With the adjectives of Figure 3, a quick patent and web search can reveal existing variations in the –adjective- bicycle frame.

Some examples of ‘adjective –bicycle frame’ are given in Figure 4 above. The parted bicycle frame on the left allows a more compact transport. The flexible bicycle frame gives better suspension. Although the search is performed on adjectives and not on verbs, it presents the functions (verbs) that are claimed. The search charts the activity in the different variations, also uncovering where no activity was found. The latter can be the more important as it gives a unique new variation to the product. This selection procedure gives some insight, though does not reduce our 19683 possible variations. For that the value equation needs to be considered.

Patent Classification
Before going deeper into value selection, consider the patent search above applied to a new example, the lighter. Within the patent database, all the lighter patents can be called forward, organised by adjective – lighter.

A further classification can be made by separating the claimed functions per variation. 345 transparent lighters of which different functions like inspection, security, or more design based features could be claimed. A multifunctional lighter can be claimed with a bottle opener, or a functional light. This sort of analysis grows the database of generic functions, that which an adjective can perform. Adjective-verb; or property-function searches prove to be an effective way to classify knowledge across application domains.

Selection by value factor
Value equates as good minus bad. Good = performance (better function); bad = 1. harm (safer or greener function), 2. interface (nicer or easier function) and 3. cost (cheaper function. The spectra transparency, colour and senses can be considered interface (design) features. This is case specific , e.g. transparency is performance in case of a window. Ignoring the interface variation, drops another 18954, bringing us to an almost manageable 729 variations. (3^6)

If the aim is strength/weight ratio for usage and transport, the variations shape and porosity will go to the left. Two properties (point and full) fall, dropping another 405 variations. The remaining options count 324, which is manageable. (3^4*4) One can argue that symmetrical is the cheapest way to produce the frame, and eliminate the symmetry variation for the value factor cost, dropping 216 options to 108. (3^3*4) Assuming the bicycle frame is to be constructed as one part, 72 variations drop to 36 possibilities. This gives (Figure 6) : Flexibility (immobile Fi, jointed Fj, flexible Ff), Surface (smooth Ss, carved Sc, 3D Carved S3) , Porosity (hollow Ph, porous Pp) and Shape (linear Sl, 3D shape Sd).

Prior Variable Selection
A classical ‘trap’ type of excersise is to ask a large audience to draw a table. 90% if not all drawings will be a solid table blade with four legs, which is indeed a table. But one, two or three legs can also make a table. The number of legs is a variable property. It is like a button to turn as shown in Figure 7.

The number of legs is one button to turn, but if inspected closely, the table is full of buttons to turn. The represent the properties that can be varied to achieve an new function. Buttons include transparency, strength, weight, flexibility, colour, surface, shape, or unity. They define the amount of variables that will form the bases of the solution space. Each setting is connected to functions.

Property Plots
As alternative to the evolutionary potential plots, in which property and function variations are mixed, it is cleaner to create property plots only. They are built as a radar diagram in which each axis is defining a property spectrum (a button to turn). The set of properties out of figure 3 creates the property plot below. Here the total of only outward moves defines 17496 variations. (Figure 8) Again, depending upon the required function, also inward variations can be considered. The beauty of a pure property plot, is that it is directly linked to a definite set of functions.

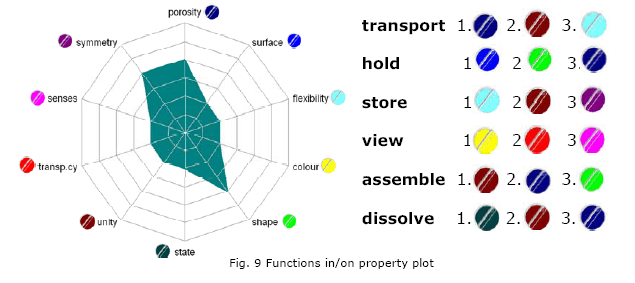
Functions in/on property plots
Whenever a property is well varied the resulting system will have new or improved functions. The other way round, when a desired function is known, a priority of variations can be given. Figure 9 shows the property radar of the bicycle frame. If the bicycle needs to be transported, a porous bicycle will be lighter, a parted will be easier to store and lighter to carry per part, and a jointed or flexible bicycle might just fit in the trunk. Holding the frame might improve through surface finish, by designing grip shapes, or even by adding holes to grip it (like a bowling ball does).

The analogy proves an easy interface to the design options. In the case of conflicting properties, solution routes can be prioritised in a similar fashion, i.e. where ‘to turn’ to solve the conflict (see DIVA Oct. 2005). For example, if the strength of the bicycle frame is compromised by making it hollow, keep turning the porosity to many small pores and the strength will restore.

Property Function Mapping
Final point, for those who enjoy Mind Mapping®, the property function relation of Directed Variation® allows a good navigation for mapping new variations.

Step 1: Write down all properties identifiable around the bicycle frame (grey).
Step 2: Define in which variation spectrum each property is and connect your initial property to the closed description. Write the variation spectrum completely, i.e. all the adjectives describing the stages (this case 3). Underline the current stage.(green)
Step 3 Evaluate the remaining stages functional, i.e. what function could they bring to the party. Note that the current stage can also bring new functions, for example the bicycle frame is hollow; it could remain hollow though add the function ‘contain’, a pump or a drink. (blue)

The inner circle defines your product property perception. The secondary green circle contains the adjectives, the property spectra. Variations in these properties will fuel new ideas, bringing better or new function; the bleu space.

Green describes the talent of the product whereas the blue zone charts the functional need and wants of the customer. The product shows off, the consumer shops.

Conclusion
Innovation through directed variation® comes down to listing your product’s properties and changing those properties along a variation spectrum. Changes are expressed in adjectives, and linked to science. Successful changes result in new or better function, these being expressed in verbs, and linked to technologies. (Part 1)

The generation of variations is exponential, though by structured elimination procedures, the drop of possibilities is likewise. Searching existing variations on the web and patent database prove insightful though incomplete.

The more drastic selection procedure is conducted by value factor. The value equation gives a four wise focus, dropping the total of available options like Belgian rain. Depending on the required function, a directed variation can eliminate the counter directed options.

Furthermore is found that the analogy ‘buttons to turn’ with ‘properties to vary’, proves very user-friendly. By purifying evolutionary plots into property plots, each axis describes a property spectrum. Depending on the desired function(s), the user is informed which ‘button to turn’.

Finally, the property function relation of Directed Variation allows a good navigation for mapping new possibilities.
Step 1: define your product perception
Step 2: create the talent of the product
Step 3: shop for functional variations

Simon Dewulf is Managing Director of CREAX; a company of creative engineers active in innovation consulting, patents studies, systematic innovation methodologies, product development, training and innovation culture coaching. With directed variation®, DIVA, CREAX brings a checklist for innovation potential that acts as a turbo for new value creation. By combining worldwide best practices in Business, Technology and Management, CREAX offers an integrated innovation method that acts as a toolbox, a philosophy and a culture for value creation. CREAX works for market leaders and innovation driven companies in all sectors including Goodyear, P&G, Shell, Masterfoods, Atlas Copco, Solvay and Bekaert. CREAX teams up Bernard Lahousse, Nele Dekeyser, Mathieu Mottrie, Johan Langenbick, Lieven De Couvreur, Nadine Rits, Lieselot Vandecappelle, Vincent Theeten, Katleen Pyck, Frederick Florizoone, Thomas Valcke, Frederick Vandendriessche, and Simon Dewulf.